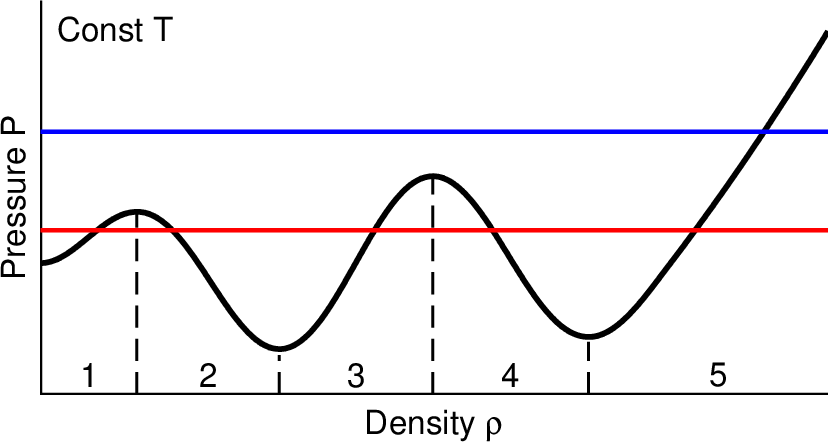
図1. 一定温度での密度と圧力の関係の模式図。
Fig. 1. A schematic view of the relation between the density and pressure at a constant temperature.
| T | 温度[K]。 The temperature [K]. |
| P | 圧力[Pa]。 The pressure [Pa]. |
 図1. 一定温度での密度と圧力の関係の模式図。 Fig. 1. A schematic view of the relation between the density and pressure at a constant temperature. |