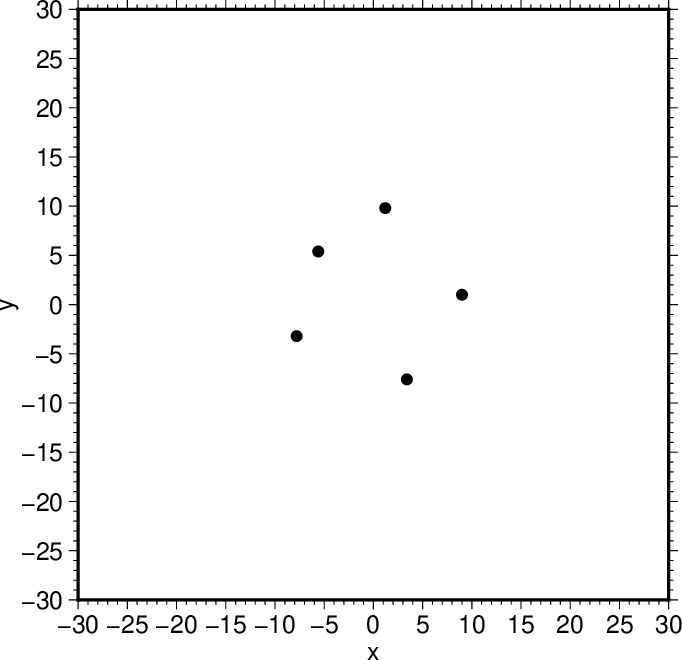
図1. 以下の説明で用いる点群。
Fig. 1. The data of points used in the description below.
| Npoints | 点の個数。 The number of points. |
| x | 点の\(x\)座標を並べた配列。 An array composed of the \(x\)-coordinates of the points. |
| y | 点の\(y\)座標を並べた配列。 An array composed of the \(y\)-coordinates of the points. |
| triangles | 求めた三角形のリストの代入先。
宣言しただけのstruct triangle ∗型変数に&を付けて与える。
関数内で配列の動的メモリの確保が行われ、
\(i\)番目の三角形要素の情報がtriangles[i]に代入される。
なお、構造体のメンバip1, ip2, ip3, p1, p2, p3のみが設定される。
三角形の3つの頂点はip1<ip2<ip3となるように並べられる。 Memory into which the list of triangles is to be inserted. Give an empty struct triangle ∗-type variable with &. Within the function, an array is allocated, and the array components triangles[i] for each \(i\) are set as representing the \(i\)th triangle. Only the members ip1, ip2, ip3, p1, p2, and p3 of the structure are set. The three vertexes for each triangle are sorted as ip1 < ip2 < ip3. |
 図1. 以下の説明で用いる点群。 Fig. 1. The data of points used in the description below. |
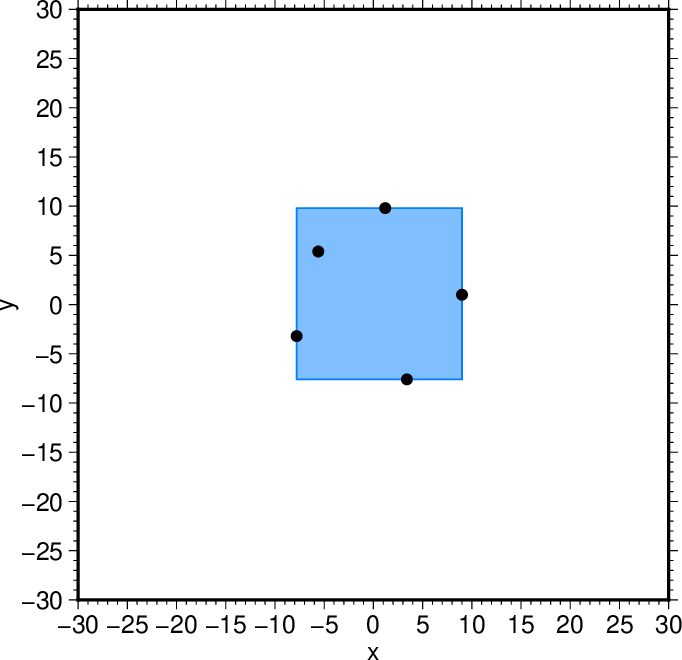 図2. 点の範囲を囲む長方形。 Fig. 2. A rectangle that bounds the points. |
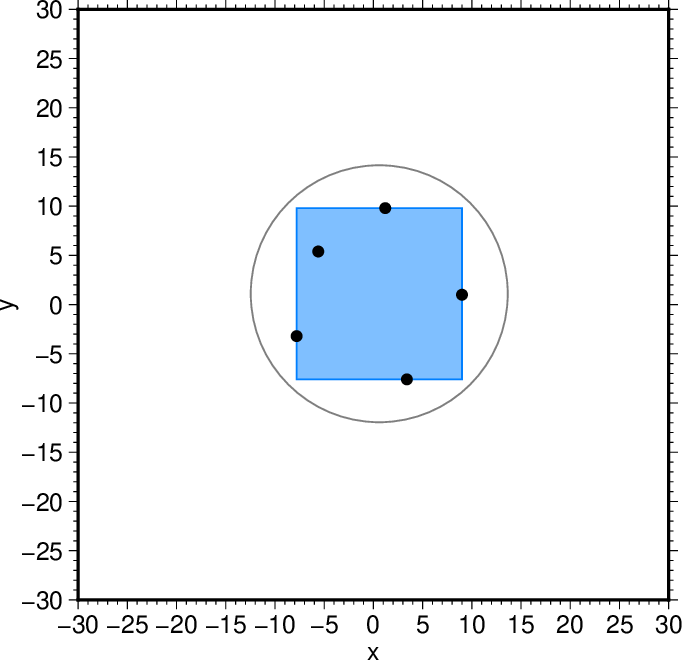 図3. 全ての点を囲む円。 Fig. 3. A circle that includes all points. |
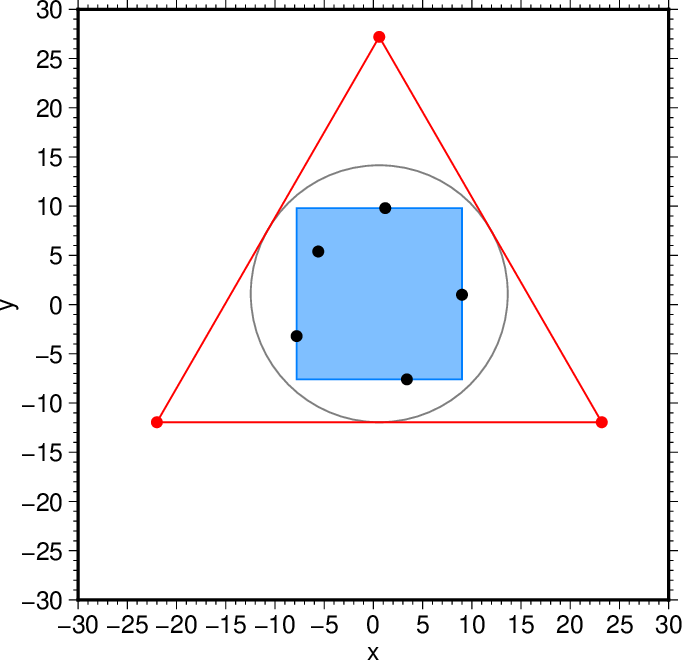 図4. 全ての点を囲む三角形。 Fig. 4. A triangle that includes all points. |
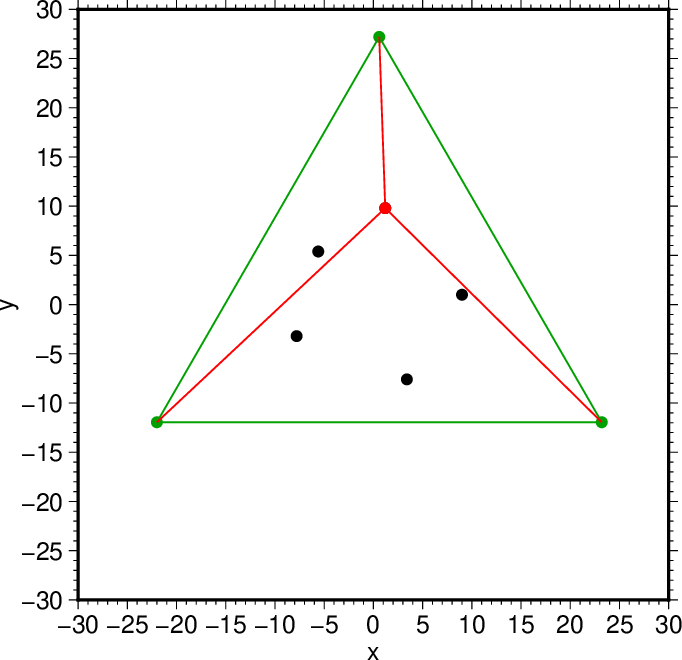 図5. 追加した点およびその点と三角形の頂点を結ぶ線(赤)。 Fig. 5. The point added and lines connecting this point with the convexes of the triangle. |
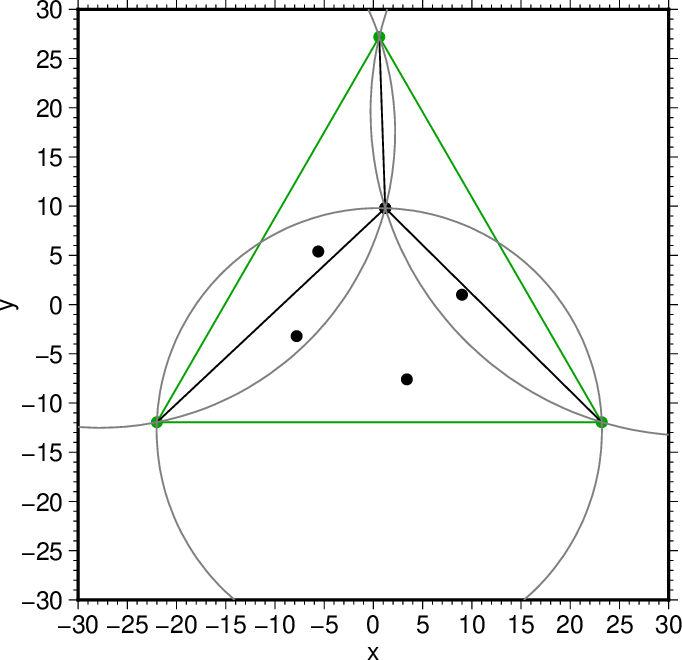 図6. 要素三角形の外接円。 Fig. 6. The circumscribed circles for elementary triangles. |
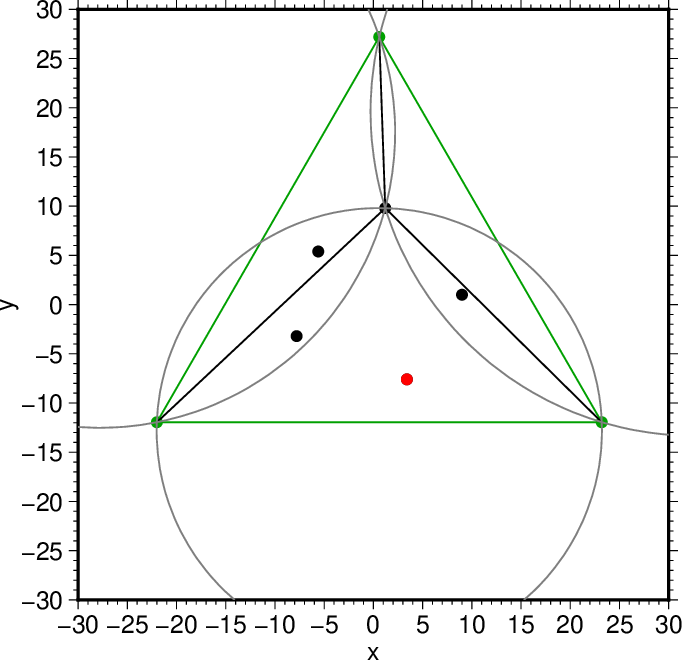 図7. 選択した2つ目の点(赤)。 Fig. 7. The 2nd point chosen (red). |
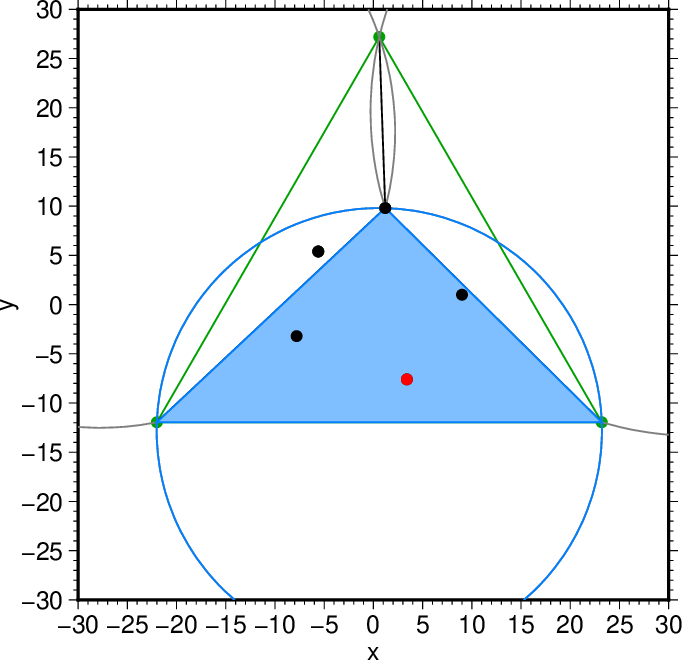 図8. 選択した2つ目の点を内包する三角形と外接円(水色)。 Fig. 8. The triangle and its circumscribed circle that include the 2nd point chosen (blue). |
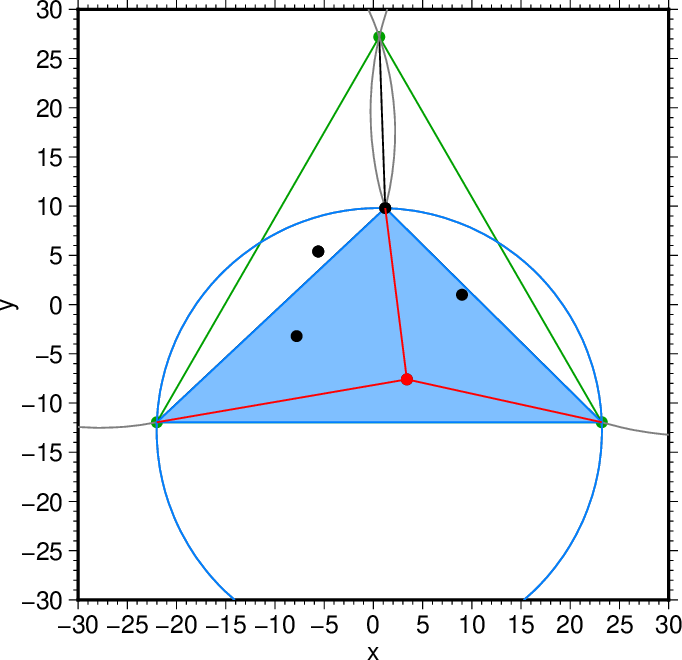 図9. 選択した2つ目の点と、注目する三角形の頂点とを結ぶ線(赤)。 Fig. 9. Lines connecting the 2nd point chosen and the convexes of the triangle to focus. |
 図10. 更新後の全ての要素三角形の外接円(灰色)。 Fig. 10. The circumscribed circles for all updated elementary triangles (grey). |
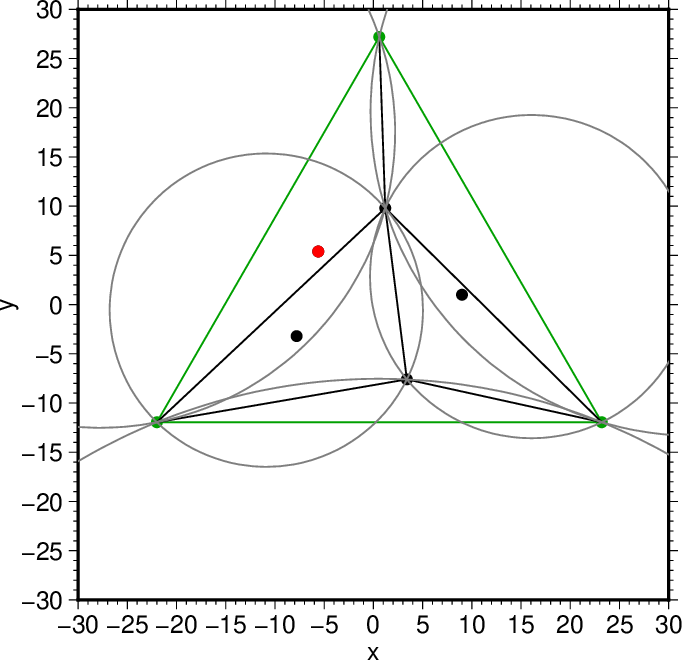 図11. 選択した3つ目の点(赤)。 Fig. 11. The 3rd point chosen (red). |
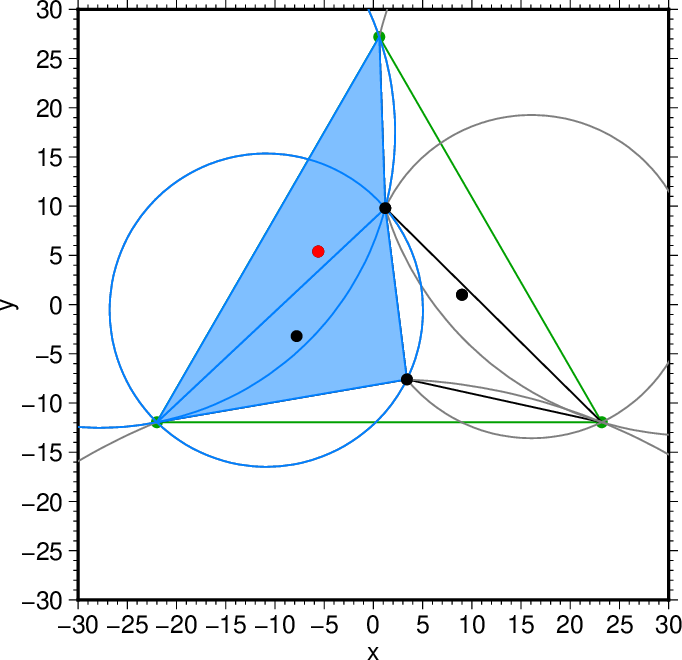 図12. 選択した3つ目の点を内包する三角形と外接円(水色)。 Fig. 12. The triangles and their circumscribed circles that include the 3rd point chosen (blue). |
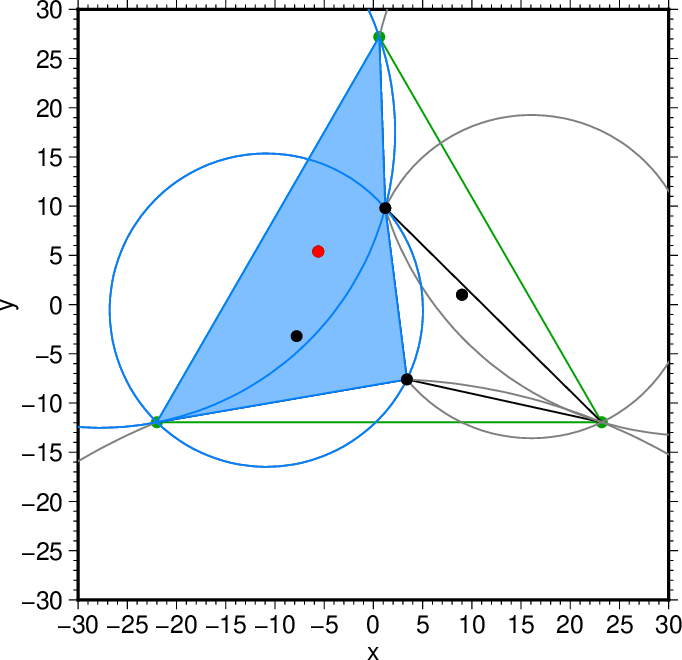 図13. 2つの三角形をマージして得られる四角形(水色)。 Fig. 13. The quadrangle obtained by merging the two triangles (blue). |
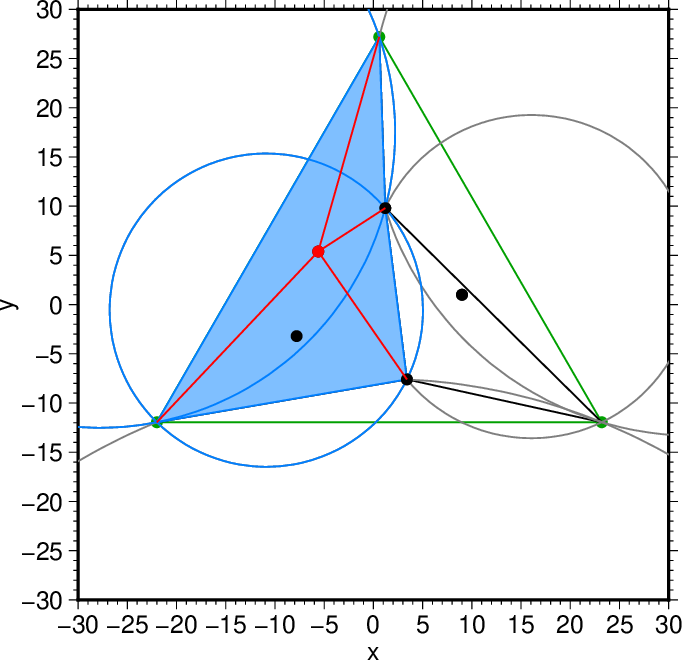 図14. 選択した3つ目の点と、注目する四角形の頂点とを結ぶ線(赤)。 Fig. 14. Lines connecting the 3rd point chosen and the convexes of the quadrangle to focus. |
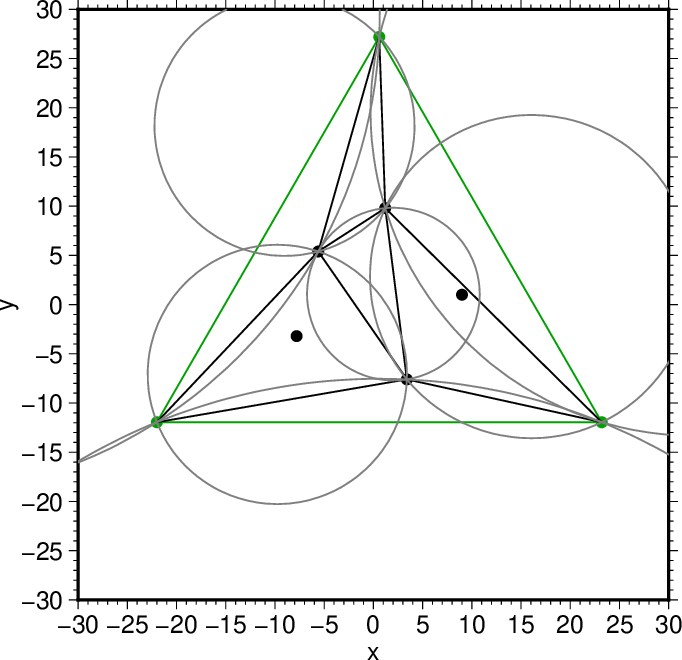 図15. 更新後の全ての要素三角形の外接円(灰色)。 Fig. 15. The circumscribed circles for all updated elementary triangles (grey). |
 図16. 選択した4つ目の点(赤)、それを内包する外接円(水色)、 その円に対応する三角形(水色)、 その三角形の頂点と4つ目の点を結ぶ線(赤)。 Fig. 16. The 4th point chosen (red), the circumscribed circle that includes this point (blue), the corresponding triangle (blue), and lines connecting the vertexes of this triangle ith the 4th point (red). |
 図17. 更新後の全ての要素三角形の外接円(灰色)。 Fig. 17. The circumscribed circles for all updated elementary triangles (grey). |
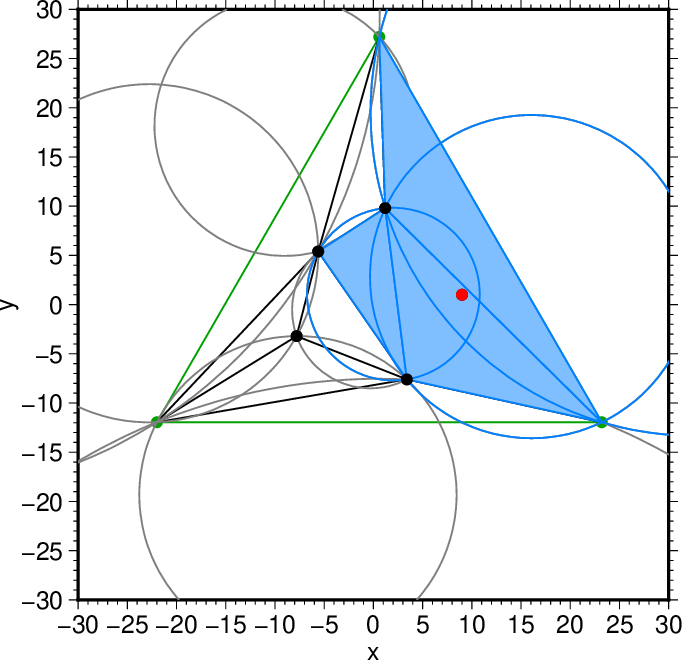 図18. 選択した5つ目の点(赤)、それを内包する外接円(水色)、 その円に対応する三角形(水色)。 Fig. 18. The 5th point chosen (red), the circumscribed circles that include this point (blue), and the corresponding triangles (blue). |
 図19. 選択した5つ目の点(赤)、それを内包する外接円(水色)、 その円に対応する三角形を合体した五角形(水色)、 五角形の頂点と5つ目の点を結ぶ線(赤)。 Fig. 19. The 5th point chosen (red), the circumscribed circles that include this point (blue), the corresponding triangles that are merged into a pentagon (blue), and lines connecting the vertexes of this pentagon with the 5th point (red). |
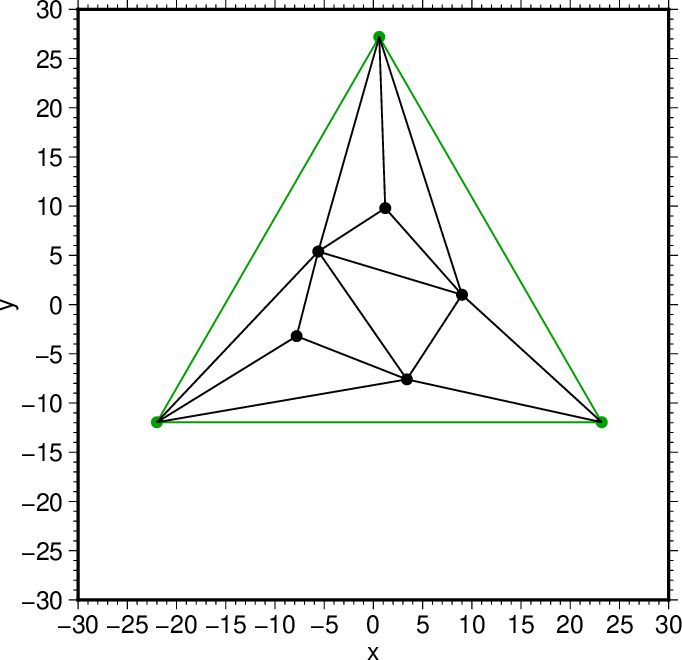 図20. これまでの操作で得られた要素三角形。 Fig. 20. The elementary triangles obtained. |
 図21. 最終的な三角形要素分割。 Fig. 21. The final decomposition of the points into triangular elements. |
 図5(再掲). Fig. 5. (reproduced) |