関数ray_horizontal_distance_1Dscalar マニュアル

(The documentation of function ray_horizontal_distance_1Dscalar)

Last Update: 2021/12/6

◆機能・用途(Purpose)

与えられた1次元速度構造のもとで 2つの深さの間の波線に沿った水平距離を計算する。
Calculate the horizontal distance along the ray between two depths using a given 1D velocity structure.

◆形式(Format)

#include <ray/calculate1Dscalar.h>
inline double ray_horizontal_distance_1Dscalar
(const double z1,const double z2,
const double p,const struct _1DvelocityStructure structure)

◆引数(Arguments)

z1	計算に用いる一方の深さ。 One depth for the calculation.
z2	計算に用いる他方の深さ。 z1との大小関係は問わないがz1と同じであってはならない。 The other depth for the calculation. This depth may be greater than or less than z1 but must not be equal to z1.
p	波線パラメータ。 A ray parameter.
structure	1次元速度構造。 A 1D velocity structure.

◆戻り値(Return value)

深さz1とz2の間の波線に沿った水平距離。波線がz1とz2のいずれかに到達しない場合はエラーとなる。
The horizontal distance along the ray between the depths z1 and z2. If the ray does not reach either of the depth z1 or z2, the program finishes as an error.

◆使用例(Example)

struct _1DvelocityStructure structure;
double distance=ray_horizontal_distance_1Dscalar (1000.0,2000.0,0.001,structure);

◆検証(Validation)

この関数によって水平距離が正しく計算できていることの検証は以下の2つのプログラムによって実施した。 2つのプログラムはいずれも、比較的複雑な速度構造のもとで地表を出発した波線が各深さに到達するまでの水平距離を計算する。プログラム1では関数ray_horizontal_distance_1Dscalarを使用する。プログラム2ではこの関数を利用せずに水平距離を計算する。なお用いている計算式の中で水平距離の解析解を導出したが、この解析解自体のチェックも兼ねてプログラム2では波線に沿った微小要素の数値積分によって水平距離を計算している。
We examined the validity of the output of this function by using the two programs shown below. The both programs compute the horizontal distances along the ray from the ground surface to various depths assuming a relatively complex velocity structure. The program 1 uses the function ray_horizontal_distance_1Dscalar, whereas the program 2 does not. The program 2 does not depend even on the analytical formula of the horizontal distances derived in Formulas used; rather, it computes the horizontal distances by numerically integrating small elements along the ray, in order to check the formula itself also.

これら2つのプログラムで用いているのは以下の速度構造である。速度勾配が増加する折れ曲がり、減少する折れ曲がり、速度勾配が負となる区間や0になる区間を一通り設けた複雑な構造であり、両者の結果が偶然に一致するとは考えにくい。
The velocity structure used in these two programs is shown below. This includes positive and negative bendings of the velocity slopes as well as sections of negative velocity slope and zero slope, to make sure that the horizontal distances computed by the two programs cannot be “by chance” consistent.

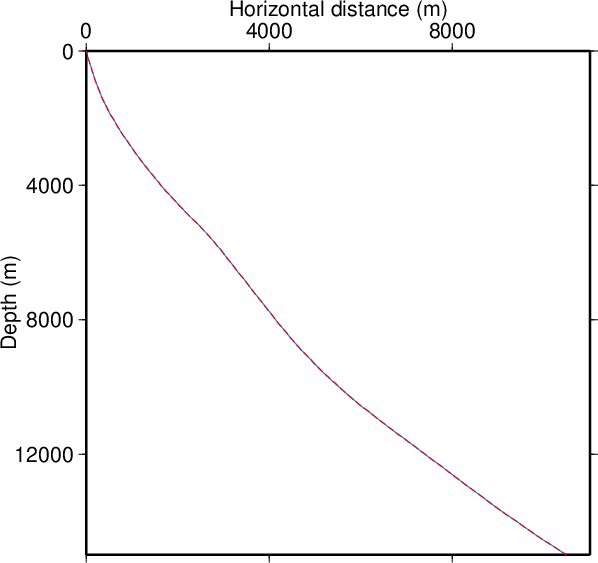
深さ(m) Depth (m)	速度(m/s) Velocity (m/s)
0	2000
1000	2500
2000	4000
5000	6000
6000	5000
8000	5000
11000	7000
13000	7000
15000	7500

プログラム1(Program 1)

#include <inc.h>

int main(void)
{
  //定数の宣言(Declare constants)
  const char outputfile[]="program1_result.dat"; //計算結果の出力先ファイル名
  const double p=0.0001; //波線パラメータ(s/m)
  const double zmax=15000.0; //水平距離を計算する深さ範囲の上限(m)
  const double zinc=100.0; //水平距離を計算する深さ間隔(m)

  //変数の宣言(Declare variables)
  struct _1DvelocityStructure structure; //仮定する速度構造
  FILE_L fp;
  double z; //波線の到達地点の深さ(m, ループ制御変数)
  double h; //水平距離(m)

  //速度構造の設定 (Set velocity structure)
  sRoute;
  structure=get_1DvelocityStructure_memory(9);
  rRoute;
  structure.depths[0]=0.0;
  structure.depths[1]=1000.0;
  structure.depths[2]=2000.0;
  structure.depths[3]=5000.0;
  structure.depths[4]=6000.0;
  structure.depths[5]=8000.0;
  structure.depths[6]=11000.0;
  structure.depths[7]=13000.0;
  structure.depths[8]=15000.0;
  structure.velocities[0]=2000.0;
  structure.velocities[1]=2500.0;
  structure.velocities[2]=4000.0;
  structure.velocities[3]=6000.0;
  structure.velocities[4]=5000.0;
  structure.velocities[5]=5000.0;
  structure.velocities[6]=7000.0;
  structure.velocities[7]=7000.0;
  structure.velocities[8]=7500.0;
  structure.slope_shallow=0.5;
  structure.slope_deep=0.1;

  //出力ファイルのオープン (Open the output file)
  sRoute;
  fp=CKfopen(outputfile,"w");
  rRoute;

  //ヘッダの出力(Write the headers)
  fprintf(fp.main, "#z(m)\thorizontal distance(m)\n");

  //深さ0mでの水平距離の出力 (Write the horizontal distance at 0 m depth)
  fprintf(fp.main,"%e\t%e\n",0.0,0.0);

  //深さ0mを出発した波線が各深さに到達するまでの水平距離を計算・出力
  //(Compute the horizontal distance at each depth along the ray starting from 0 m depth)
  for(z=zinc;doublecmp(z,zmax)<=0;z+=zinc){
    sRoute;
    h= ray_horizontal_distance_1Dscalar(0.0,z,p,structure);
    rRoute;
    fprintf(fp.main, "%e\t%e\n",z,h);
  }

  //出力ファイルのクローズ (Close the output file)
  sRoute;
  CKfclose(fp);
  rRoute;

  //終了処理(Finish)
  return 0;
}

プログラム2(Program 2)

#include <inc.h>

int main(void)
{
  //定数の宣言(Declare constants)
  const char outputfile[]="program2_result.dat"; //計算結果の出力先ファイル名
  const double p=0.0001; //波線パラメータ(s/m)
  const double zmax=15000.0; //水平距離を計算する深さ範囲の上限(m)
  const double zinc=100.0; //水平距離を出力する深さ間隔(m)
  const double dz=0.01; //水平距離計算に用いる差分刻み幅(m)
  const double z0=0.0; //以下、速度構造の定義
  const double z1=1000.0;
  const double z2=2000.0;
  const double z3=5000.0;
  const double z4=6000.0;
  const double z5=8000.0;
  const double z6=11000.0;
  const double z7=13000.0;
  const double z8=15000.0;
  const double v0=2000.0;
  const double v1=2500.0;
  const double v2=4000.0;
  const double v3=6000.0;
  const double v4=5000.0;
  const double v5=5000.0;
  const double v6=7000.0;
  const double v7=7000.0;
  const double v8=7500.0;

  //変数の宣言(Declare variables)
  FILE_L fp;
  double z; //波線の到達地点の深さ(m, ループ制御変数)
  double v; //その深さでの速度(m/s)
  double theta; //その深さでの波線の角度(rad)
  double dh; //その深さでのdzに対応する水平距離(m)
  double h; //水平距離(m)

  //出力ファイルのオープン (Open the output file)
  sRoute;
  fp=CKfopen(outputfile,"w");
  rRoute;

  //ヘッダの出力(Write the headers)
  fprintf(fp.main, "#z(m)\thorizontal distance(m)\n");

  //深さ0mを出発した波線が各深さに到達するまでの水平距離を計算・出力
  //(Compute the horizontal distance at each depth along the ray starting from 0 m depth)
  h=0.0;
  for(z=0.0;doublecmp(z,zmax)<=0;z+=dz){

    //水平距離の出力 (Write the horizontal distance)
    if(isdividable(z,zinc)) fprintf(fp.main,"%e\t%e\n",z,h);

    //現在の深さでの速度の計算 (Calculate the velocity at current depth)
    if(z<=z1){
      v=v0+(v1-v0)∗(z-z0)/(z1-z0);
    }else if(z<=z2){
      v=v1+(v2-v1)∗(z-z1)/(z2-z1);
    }else if(z<=z3){
      v=v2+(v3-v2)∗(z-z2)/(z3-z2);
    }else if(z<=z4){
      v=v3+(v4-v3)∗(z-z3)/(z4-z3);
    }else if(z<=z5){
      v=v4+(v5-v4)∗(z-z4)/(z5-z4);
    }else if(z<=z6){
      v=v5+(v6-v5)∗(z-z5)/(z6-z5);
    }else if(z<=z7){
      v=v6+(v7-v6)∗(z-z6)/(z7-z6);
    }else{
      v=v7+(v8-v7)∗(z-z7)/(z8-z7);
    }

    //現在の深さでの波線角度の計算 (Calculate the ray angle at current depth)
    theta=asin(p∗v);

    //dzの深さ変化に対応する水平距離の計算
    //(Calculate the horizontal distance along the ray corresponding to the depth change dz)
    dh=dz∗tan(theta);

    //水平距離の更新 (Update the horizontal distance)
    h+=dh;
  }

  //出力ファイルのクローズ (Close the output file)
  sRoute;
  CKfclose(fp);
  rRoute;

  //終了処理(Finish)
  return 0;
}

これらのプログラムによって求めた水平距離を下図に示す。青の実線はプログラム1からの出力、赤の破線はプログラム2からの出力である。両者が一致していることから関数および計算式は正しいと思われる。
The figure below shows the results from these programs; the blue solid line represents the output from the program 1, and the red dashed line does that from the program 2. These results are consistent, suggesting that the function and the formula are correct.