ヒープソートのアルゴリズム

(The heap sort algorithm)

◆分岐構造と親要素・子要素 (A branch structure and parent and child components)

ヒープソートのアルゴリズムを一般論として書くとややこしいので、以下では10個の要素から成る配列 data[0], data[1], …, data[9]を考える。具体例として表1の配列を考える。
Since a general description for the heap sort algorithm would be complicated, let us consider an array composed of 10 components, data[0], data[1], …, data[9]. As an example, let us consider an array given in Table 1.

表1: 以下で考える配列の例。
Table 1: An array example considered below.

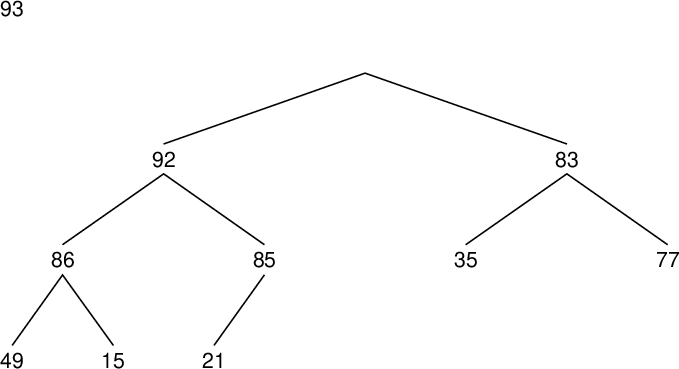
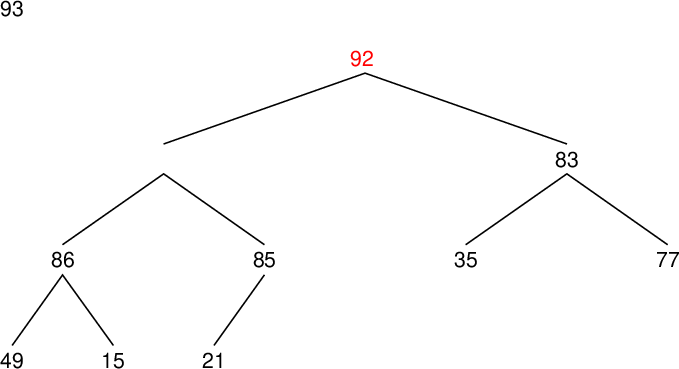
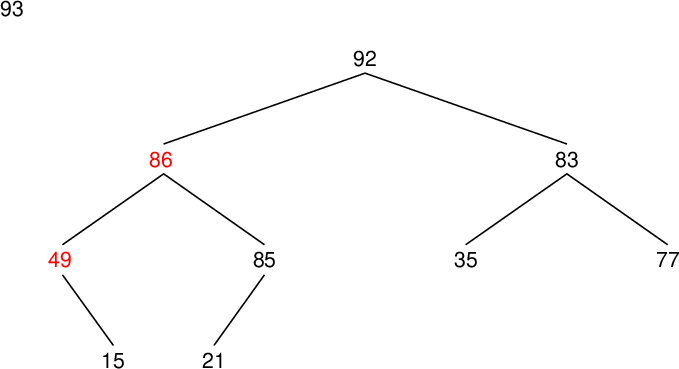
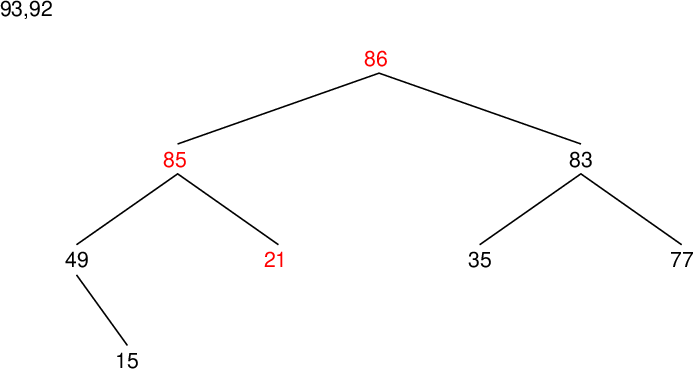
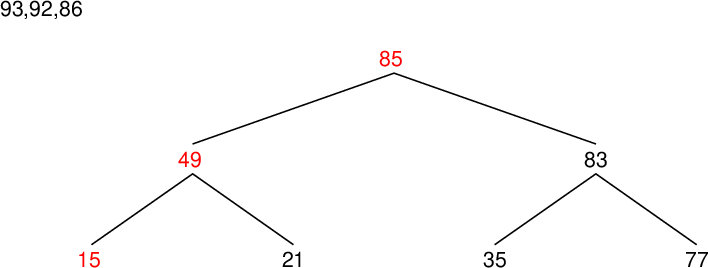
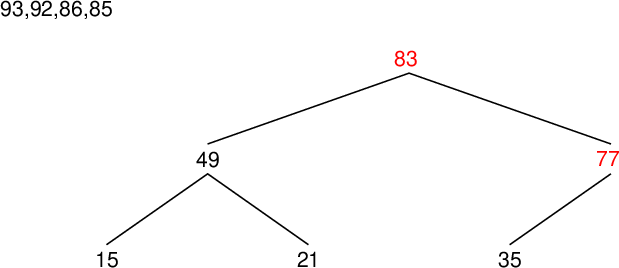
配列要素 Array component	値 Value
data[0]	83
data[1]	85
data[2]	77
data[3]	15
data[4]	93
data[5]	35
data[6]	86
data[7]	92
data[8]	49
data[9]	21

ヒープソートではまず、配列要素を図1のような枝状に並べる (これは実際にプログラムで何かをするのではなく、単に頭の中でこのようなデータ構造を想像するということである)。
As the first step of the heap sort, the array components are deployed into a branch structure shown in Fig. 1; this is not to do something in the program but to only imagine this structure in the brain.

図1: ヒープソートで用いるデータ構造
Fig. 1: A data structure considered in the heap sort.

ここで、data[0]とdata[1]とdata[2]、data[1]とdata[3]とdata[4]のように 2本の枝に分岐した3つのデータの組の中で上にあるものを親要素、下にあるものを子要素と呼ぶ。 data[0]とdata[1]とdata[2]の組合せであれば data[0]が親要素でdata[1]とdata[2]が子要素である。またdata[1]とdata[3]とdata[4]の組合せであれば data[1]が親要素でdata[3]とdata[4]が子要素である。
Now, let us focus on the three array components connected by each branch, such as a group of data[0], data[1], and data[2], or a group of data[1], data[3], and data[4]. Among the three components, the data located at the top is called a parent component, and the other two are called child components. For example, data[0] is the parent component and the other two are child components among the combination of data[0], data[1], and data[2]. In the same way, data[1] is the parent component and the other two are child components among the combination of data[1], data[3], and data[4].

ヒープソートでは親要素と子要素の交換を頻繁に行う。配列要素番号を直接用いると分かりにくいので sort.hでは親要素と子要素を対応付ける関数を定義している。

heap_leftChildは親要素の配列要素番号を与えて左側の子要素の配列要素番号を返す関数である。
heap_rightChildは親要素の配列要素番号を与えて右側の子要素の配列要素番号を返す関数である。
heap_parrentは子要素の配列要素番号を与えて親要素の配列要素番号を返す関数である。

図1から容易に分かるように

heap_leftChild(\(n\))\(=2n+1\)
heap_rightChild(\(n\))\(=2n+2\)

であり、heap_parrent(\(n\))は

\(n\)が奇数のとき\((n-1)/2\)
\(n\)が偶数のとき\((n-2)/2\)

である。
In the heap sort, the parent and child components are replaced again and again. To be comprehensive, functions to relate the parent and child components are defined in sort.h as below:

function heap_leftChild returns the index of the left child component given the index of a parent component;
function heap_rightChild returns the index of the right child component given the index of a parent component; and
function heap_parrent returns the index of the parrent component given the index of a child component.

Fig. 1 indicates that heap_leftChild(\(n\))\(=2n+1\) and heap_rightChild(\(n\))\(=2n+2\), and heap_parrent(\(n\)) would be \((n-1)/2\) and \((n-2)/2\) for odd and even \(n\), respectively.

◆ヒープ構造の作成 (Creating a heap structure)

ヒープソートでは図1のデータを親要素が子要素よりも大きくなるように並べ替える。このような構造をヒープ構造という。ヒープ構造を作るには配列の後の要素から順に、親要素と比較して値が大きければ親要素と交換するという処理を交換が生じなくなるまで繰り返せば良い。
In the heap sort, the data in Fig. 1 are replaced such that each parrent component is larger than the two child components of it. This structure is called a heap structure. The heap structure is created by a comparison of each array component with its parent component and replacement of them if the parent component is smaller. This comparison and replacement, backward from the and to front array components, is repeated until no more replacement occurs.

表1のデータを具体例としてこの流れを説明すると以下のようになる。まず表1のデータを図1の形式に並べると図2のようになる。
Below is an explanation of this flow for the example of Table 1. First, the data in Table 1 is deployed in the format of Fig. 1; the result is shown in Fig. 2.

図2: 表1のデータを図1の形式で並べたデータ構造。
Fig. 2: A data structure for the data of Table 1 in the format of Fig. 1.

配列の最終要素(21)をその親要素(93)と比較する(下図の赤字部分)。親要素の方が大きいのでこのままにする。
Compare the final array component (21) with its parent component (93), which are shown red in the figure below. Since the parrent component is larger, the values are not replaced.

次に配列の後から2番目の要素(49)をその親要素(15)と比較する。親要素の方が小さいので49と15を入れ替える。
Next, compare the second final array component (49) with its parent component (15). Since the parent component is smaller, the two values are replaced.

次に配列の後から3番目の要素(92)をその親要素(49)と比較する。親要素の方が小さいので92と49を入れ替える。
Next, compare the third final array component (92) with its parent component (49). Since the parent component is smaller, the two values are replaced.

以下同様にして配列要素を親要素と比較し、親要素の方が小さければ交換するということを繰り返していく。この処理を一覧にすると表2のようになる。
In the same way, replace each array component with its parent component, and if the parent component is smaller, the two values are replaced. This series of processings is listed in Table 2.

表2: 表1の配列に対して行う1回目のループでのチェックと置換。
Table 2: Checks and replacements for the array in Table 1 in the 1st loop.

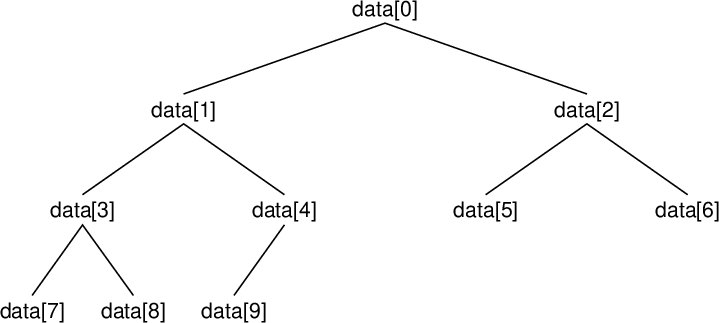
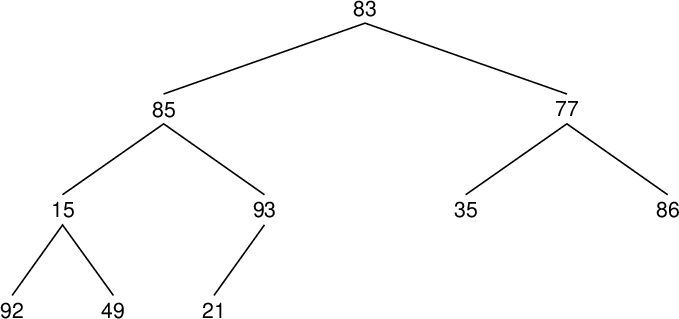
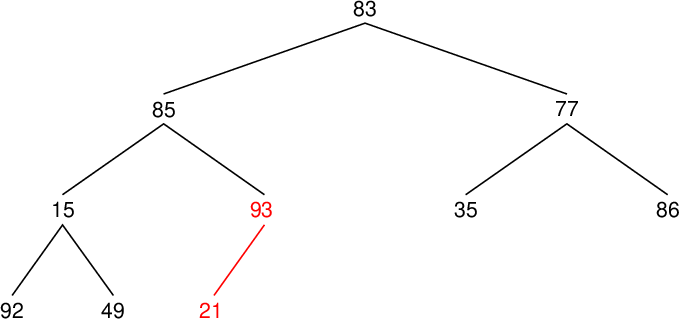
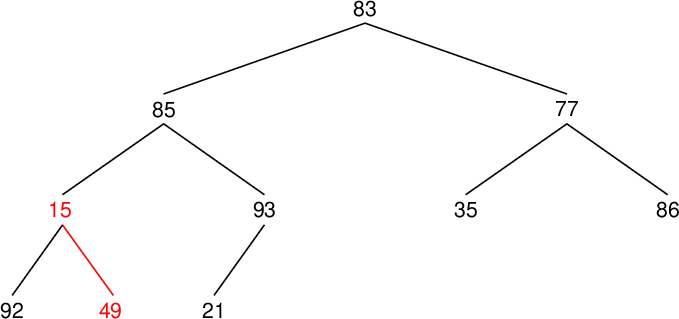
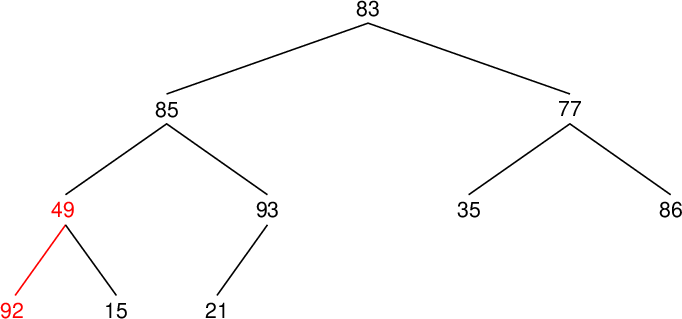
配列要素番号 Array component index	値 Value	親要素の値 Value of parent component	置換の有無 Whether to replace (○) or not
data[9]	21	93
data[8]	49	15	○
data[7]	92	49	○
data[6]	86	77	○
data[5]	35	86
data[4]	93	85	○
data[3]	92	93
data[2]	86	83	○
data[1]	93	86	○

この一連の処理が終わった段階では図3の配置になる。
The layout of the data after this series of processings is shown in Fig. 3.

図3: 1回目のループの処理(表2)が終わった時点でのデータ構造。
Fig. 3: A data structure after the 1st loop in Table 2.

次に、この図3のデータ構造に対して再び配列の最終要素から順に親要素と比較して親要素の方が小さければ交換するという処理を行う。具体的な処理を列挙すると表3のようになる。
Next, the comparison of each array component with its parent component and the replacement if the parent component is smaller are repeated again backward from the end to front array components. This procedure is listed explicitly in Table 3.

表3: 図3のデータに対して行う2回目のループでのチェックと置換。
Table 3: Checks and replacements for the data in Fig. 3 in the 2nd loop.

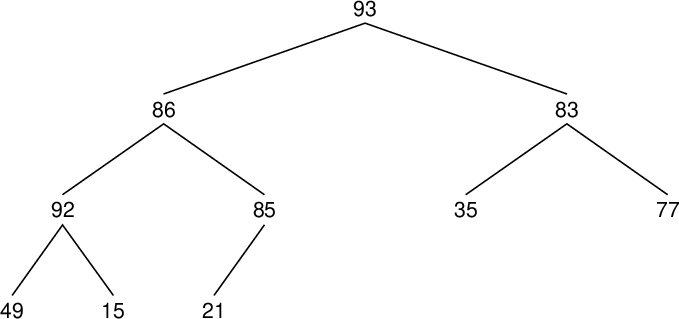
配列要素番号 Array component index	値 Value	親要素の値 Value of parent component	置換の有無 Whether to replace (○) or not
data[9]	21	85
data[8]	15	92
data[7]	49	92
data[6]	77	83
data[5]	35	83
data[4]	85	86
data[3]	92	86	○
data[2]	83	93
data[1]	92	93

この処理の結果は図4のようになる。
The result of this processing is shown in Fig. 4.

図4: 2回目のループの処理(表3)が終わった時点でのデータ構造。
Fig. 4: A data structure after the 2nd loop in Table 3.

図4のデータ構造に対して再び配列の最終要素から順に親要素と比較して親要素の方が小さければ交換するという処理を行う。具体的な処理を列挙すると表4のようになる。
For the data structure of Fig. 4, the comparison of each array component with its parent component and the replacement if the parent component is smaller are repeated again backward from the end to front array components. This procedure is listed explicitly in Table 4.

表4: 図4のデータに対して行う3回目のループでのチェックと置換。
Table 4: Checks and replacements for the data in Fig. 4 in the 3rd loop.

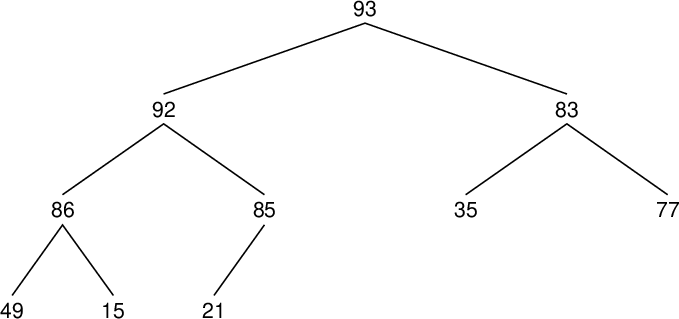
配列要素番号 Array component index	値 Value	親要素の値 Value of parent component	置換の有無 Whether to replace (○) or not
data[9]	21	85
data[8]	15	86
data[7]	49	86
data[6]	77	83
data[5]	35	83
data[4]	85	92
data[3]	86	92
data[2]	83	93
data[1]	92	93

今度は子要素と親要素の置換が1度も生じなかった。このことから図4が既にヒープ構造になっていると判定でき、ヒープ構造判定に関するループを抜けてプログラムは次のステージへと進むことになる。
No replacement between the child and parent components occurred, which means that Fig. 4 is already a heap structure. Thus the program exits from the loop to create a heap structure and proceed to the next stage.

sort.hではヒープ構造を作成する関数として create_heap_structureが定義されている。この関数ではデータそのものの並べ替えは行わない。元のデータが後で必要になることもあるし、単に並べ替えた結果ではなくどの配列要素がどの場所に移ったのかを知る必要がある場合も想定されるからである。元々のデータがdata[0], data[1], … data[\(N-1\)]であったとして、関数create_heap_structureではdataの配列要素の交換は行わず、 data[index[0]], data[index[1]], … data[index[\(N-1\)]] がヒープ構造をなすように配列要素番号を対応付ける新しい配列indexを作成する。すなわち、ヒープ構造に並べ替えたときに \(n+1\)番目に来るべきdataの配列要素番号がindex[\(n\)]であり、そのリストを戻り値として返すのが関数create_heap_structureである。
In sort.h, a function create_heap_structure is defined to create a heap structure. This function does not sort the data because the original data or relations between old and new array components may be needed later. Instead of sorting the data, the function creates a new array index such that data[index[0]], data[index[1]], … data[index[\(N-1\)]] constitute a heap structure, where data[0], data[1], … data[\(N-1\)] are the original data. Here index[\(n\)] represents the index of array data which should be at the \((n+1)\)th place to construct a heap structure, and this new array index is returned by the function create_new_structure.

◆降順での値の取り出し (Extracting the values in descending order)

ヒープ構造では子要素同士の大小関係は分からないが、親要素が子要素よりも大きいという大小関係から一番上のデータが全体の最大値であることが分かる。図4であれば一番上にある93という値が全体の最大値である。これを最大値として取り出す。
In the heap structure, relations between child components are unknown. However, since each parent component is larger than its child components, the data at the top is necessarily the maximum of all the data. In Fig. 4, the value of 93 at the top of the structure is the maximum. Extract this value.

93が抜けて空いたスペースには2つの子要素(92と83)のうちの大きい方(92)を上げる。
The resultant blank space, where the value of 93 existed, is filled with the larger one of the two child components. In this case the two child components are 92 and 83, and the larger one is 92.

92が親要素に繰り上がることで空いたスペースには 92の2つの子要素(86と85)のうちの大きい方(86)を上げる。そして86が抜けたスペースにはその2つの子要素(49と15)のうちの大きい方(49)を上げる。このようにして作られる構造(図5)を見ると再びヒープ構造になっていることが分かる。
The movement of 92 to the higher position resulted in a new blank space, which is filled with the larger one of the two child components of 92, in this case 86. Then the space originally occupied by 86 becomes a new blank, which is filled with the larger one of the two child components of 86, in this case 49. The resultant structure, shown in Fig. 5, is again a heap structure.

図5: 図4の最大値(93)を取り出して空いたスペースを大きい方の子要素で順々に埋め合わせたデータ構造。
Fig. 5: A data structure obtained by extracting the maximum in Fig. 4 (93) and consequently filling the blank spaces by the larger child components.

再び最大値(92)を取り出して、空いたスペースを子要素の大きい方で順々に埋める(図6)。
Extract the maximum (92) again, and consequently fill the blank spaces caused by moving parent components with the larger one of the child components (Fig. 6).

図6: 図5の最大値(92)を取り出して空いたスペースを大きい方の子要素で順々に埋め合わせたデータ構造。
Fig. 6: A data structure obtained by extracting the maximum in Fig. 5 (92) and consequently filling the blank spaces by the larger child components.

以下、同様の処理を繰り返す。
The same procedure is repeated.

これを繰り返していくことで降順に並んだデータ列を取り出すことができる。
Repeating this procedure gives the data in a descending order.

この段階でもヒープ構造の作成時と同様、sort.hではデータ自体の並べ替えは行わず、データを並べ替えるために必要な配列要素番号の取り出し順リストを作成する。これを行うのが関数sort_heap_dataであり、元々のデータがdata[0], data[1], …, data[\(N-1\)]であったときに data[index[0]], data[index[1]], …, data[index[\(N-1\)]] が降順に並ぶような配列要素番号の対応表indexを返す。
In this stage, the data are not sorted in sort.h, as in the stage of creating the heap structure. Instead, a list of order of extracting the array indices to sort the data. This task is done by function sort_heap_data, which creates a new array index such data data[index[0]], data[index[1]], …, data[index[\(N-1\)]] are descending order, where data[0], data[1], …, data[\(N-1\)] are the original data.

関数sort_heap_dataではデータ配列に加え、関数create_heap_structureが返すヒープ構造の配列要素順情報を使用する。すなわち、関数create_heap_structureを用いてまずヒープ構造を取得し、次にその情報を使って関数sort_heap_dataによりソートを行うという2段構えである。ソートのたびに2つの関数を呼び出さなければならないのは不便であるので、関数create_heap_structureとsort_heap_dataを内部で連続して呼び出す関数として heap_sortを用意してある。これを用いれば1発でソートができるので、通常は関数heap_sortを用いれば良い。
Function sort_heap_data relies not only on the data array but also the order of array indices in the heap structure given by function create_heap_structure. Namely, first the function create_heap_structure is needed to be called to obtain a heap structure, after which the function sort_heap_data is used to sort the data. To simplify this two-step approach, a function heap_sort is available; this function internally calls the functions create_heap_structure and sort_heap_data so that the users have to call only this single function. In summary, the function heap_sort should normally be used to sort a data.