FDM_1D_verticalコマンドの検証

1. 均質媒質での計算

(Validation of FDM_1D_vertical command; 1. Calculation in a uniform medium)

問題設定 (Problem setting)

一様な地震波速度\(V\)を持つ均質媒質を考える。 地表面の標高を\(z=0\)、 ボアホール観測点の標高を\(z=-h\) (\(h>0\))とする。 観測点に鉛直下方から入射した波を \[\begin{equation} V_{in}(-h,t)=f(t) \label{eq.Vin.station} \end{equation}\] とする。この波が地表に到着するときには走時\(h/V\)だけ遅れるので \[\begin{equation} V_{in}(0,t)=f(t-h/V) \label{eq.Vin.surface} \end{equation}\] となる。この波は地表で反射して反射波 \[\begin{equation} V_{reflect}(0,t)=f(t-h/V) \label{eq.Vreflect.surface} \end{equation}\] を生成する。この反射波は鉛直下方へと伝搬し、ボアホール観測点の位置では \[\begin{equation} V_{reflect}(-h,t)=f(t-2h/V) \label{eq.Vreflect.station} \end{equation}\] となる。入射波と反射波を足したものが観測される波形であるので、 ボアホール観測点では \[\begin{equation} V(-h,t)=V_{in}(-h,t)+V_{reflect}(-h,t)=f(t)+f(t-2h/V) \label{eq.V.station} \end{equation}\] 地表では \[\begin{equation} V(0,t)=V_{in}(0,t)+V_{reflect}(0,t)=2f(t-h/V) \label{eq.V.surface} \end{equation}\] となるはずである。差分計算でこれを再現できるかを確かめる。
We consider a uniform medium of seismic velocity \(V\), and assume the ground surface and borehole station altitudes to be \(z=0\) and \(z=-h\) (\(h>0\)), respectively. Assume that an incident wave that arrived the borehole station from below is expressed by Eq. (\ref{eq.Vin.station}). This wave propagates to the surface with a travel time \(h/V\), resulting in the wave at the ground surface given by Eq. (\ref{eq.Vin.surface}). It reflects at the surface, generating a reflected wave expressed by Eq. (\ref{eq.Vreflect.surface}). This wave propagates downward, giving (\ref{eq.Vreflect.station}) at the location of the borehole station. The summation of the indicent and reflected waves are observed, which is (\ref{eq.V.station}) at the borehole station and (\ref{eq.V.surface}) at the ground surface. We examine whether this is reproduced by the FDM calculation.
具体的な計算手順は以下の通りである。 適当な関数形\(f(t)\)を考え、 ボアホール観測点での波形(\ref{eq.V.station})を作成する。 これを用いて差分法により地表での波形を計算する。 その結果が(\ref{eq.V.surface})式の予想と一致するかを確かめる。
The calculation step is as follows. We assume a function \(f(t)\), and create the waveform at the borehole station by Eq. (\ref{eq.V.station}). We then compute the waveform at the ground surface using the FDM. We finally compare the result with the waveform at the surface expected by Eq. (\ref{eq.V.surface}).
以下では地震波速度\(V=2000\) m/s、 ボアホール観測点の深さは\(h\sim 1000\) mとする。 なお\(h/\Delta z\)が整数\(+1/2\)とならなければならないので \(\Delta z\)の値に応じて\(h\)も僅かに変化する。 作成する観測波形の時間刻みは実際の観測データにおいて最も一般的な0.01 s刻みとする。 ナイキスト周波数は50 Hzであり、これに対応する波長は40 mとなる。 また、5秒間の波形を計算する。
Below, a seismic wave velocity \(V=2000\) m/s and a borehole station depth \(h\sim 1000\) m are used. Note that the exact value of \(h\) changes slightly according to the value of \(\Delta z\) to satisfy the requirement that \(h/\Delta z\) is an integer \(+1/2\). A 0.01 s interval is used for the sampling interval of the observed waveform to create, which is most general in the actual observed data. The Nyquist frequency is 50 Hz, and corresponding wave length is 40 m. We calculate 5-s-long waveforms.

1-1. 時定数0.1秒の1周期cos関数
(A one-cycle cos function of 0.1 s time constant)

ボアホール観測点と地表の間の走時は\(h/V=0.5005\) sである。 \(f(t)\)としてこれよりも十分に短い時定数をもつ関数を考える。 このとき(\ref{eq.V.station})式の第1項(入射波)と第2項(反射波)は 分離した波形になる。 ここでは単純な関数形として1周期cos関数 \[\begin{equation} f(t)= \begin{cases} 0 & (t<0) \\ \frac{1-\cos(2\pi t/\tau)}{2} & (0\leq t\leq \tau) \\ 0 & (\tau<t) \end{cases} \label{eq.cos} \end{equation}\] を考える。\(\tau\)が時定数を表し、ここでは\(\tau=0.1\) sである。
The travel time between the borehole station and ground surface is \(h/V=0.5\) s. We consider \(f(t)\) whose time scale is sufficiently shorter than this travel time. In this case, the 1st term (incident wave) and 2nd term (reflected wave) of Eq. (\ref{eq.V.station}) are separated in the waveform. As a simple function form, we here consider a one-cycle cos function given by Eq. (\ref{eq.cos}). Here, \(\tau\) represents the time constant, which is \(\tau=0.1\) s in this case.
まずは差分計算のグリッドサイズとして\(\Delta z=2\) mを用いた。 この場合、ナイキスト周波数に対応する波長の中に20グリッドが入ることになる。 観測点の深さは\(h=1001\) mとした。 差分計算の時間刻みは安定条件 \(\Delta t<\Delta z/(\sqrt{3}V)\sim 5.8\times 10^{-4}\) s を満たすように\(\Delta t=5\times 10^{-4}\) sとした。
We first used a grid size \(\Delta z=2\) m for the FDM calculation. In this case, there are 20 grids in the wave length corresponding to the Nyquist frequency. A station depth of \(h=1001\) m is used. The time stepping of the FDM calculation must satisfy the stability condition \(\Delta t<\Delta z/(\sqrt{3}V)\sim 5.8\times 10^{-4}\) s, and we used \(\Delta t=5\times 10^{-4}\) s.
結果を図1に示す。 (a)は地表での波形、(b)はその拡大図、 (c)はボアホール観測点での波形、(d)はその拡大図を示している。 青線は(\ref{eq.V.station})(\ref{eq.V.surface})式に基づく理論波形、 赤線は実際にFDM_1D_verticalコマンドで計算した波形である。 ボアホール観測点の位置においても理論波形と異なるのは 補間を行っているためである。
The result is shown in Fig. 1, where (a) is the waveforms at the ground surface, (b) is an extension of it, (c) is the waveforms at the borehole station, and (d) is an extension. Blue lines show theoretical waveforms based on Eqs. (\ref{eq.V.station}) and (\ref{eq.V.surface}), and red lines do waveforms calculated by FDM_1D_vertical command. The calculated waveforms (red) are different from theoretical ones (blue) even at the borehole station location because the waveforms are interpolated.

図1(Fig. 1)

まず図1aを見ると計算波形(赤)と理論波形(青)はほぼ重なっており、 大まかには正しい波形が得られたことが分かる。 しかしここで疑問が湧く。 FDM_1D_verticalコマンドでは ボアホール観測点での波形を境界条件として与えて計算する。 観測された波群が上向きの波か、下向きの波かについては一切の情報を与えていない。 それにも関わらずボアホール観測点での\(t=1\) sでのパルスが 地表で\(t=1.5 s\)に現れないのは何故だろうか。 この疑問に答えることが更なる考察を行う上での鍵になるので まずこの問題について考えよう。
Fig. 1a shows that the calculated (red) and theoretical (blue) waveforms are almost fitted, indicating that a roughly correct waveform was obtained. However, a question arises here. The FDM_1D_vertical command uses the observed waveform as a boundry condition. No information is given to the program regarding whether each observed wave packet is upward or downward propagating wave. Nevertheless, why the pulse at \(t=1 s\) at the borehole station does not cause a pulse at \(t=1.5 s\) at the ground surface? Let us first solve this question, as it is the key to continue further discussion.
図2には各時刻でのスナップショットをまとめて 時刻\(t\)、位置\(z\)の関数としての速度場をプロットした。 これを見ると時刻\(t=0\) sでのパルスが上向きに伝搬し、 \(t=0.5\) sに地表面で反射し、 \(t=1\) sにボアホール観測点まで戻ってくる様子が分かる。
Fig. 2 shows the velocity field as a function of time \(t\) and location \(z\), created by gathering the snapshots at individual time moments. This figure shows that the pulse at time \(t=0\) s propagates upward, arrives at the ground surface at \(t=0.5\) s, where it reflects and then returns back to the borehole station at \(t=1\) s.

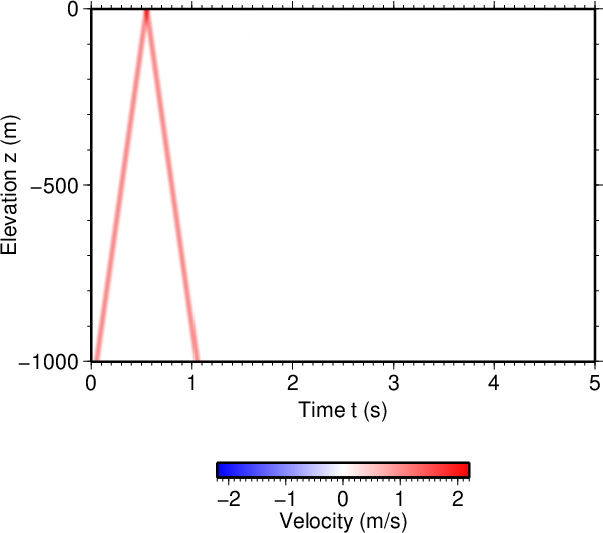
図2(Fig. 2)

実はこの反射波によって\(t=1\) sでのパルスが説明できてしまうので 新たな波群を生成しないのである。 すなわち、ボアホール観測点での波形そのものがソースになるのではなく、 観測波形からそれ以前の時刻の波群の構造応答によって説明できる分を差し引いた 残りの分がソースになるという仕組みになっている。
The key is that the pulse at \(t=1\) s can be explained by this reflected wave, thereby not producing a new wave packet. The source to the wave field is not the observed waveform itself; instead, only the remaining part of the waveform which cannot be explained by the structural response of wave packets before that time acts as the source.
このことを確かめるために別の計算を行ってみた。 図3では観測波形として時刻\(t=0\) sのパルスのみを与えた場合の 計算結果を示している。 図4はこの計算における波動場を示す。 この例では時刻\(t=0\) sのパルスの構造応答として \(t=1\) sに現れるはずのパルスが観測されていない。 そこで、このパルスを打ち消す逆符号のパルスが\(t=1\) sに入ったと解釈され、 その逆符号のパルスが\(t=1\) sから\(t=2\) sにかけて地下を伝搬している。 以後同様のことが繰り返されている。 この結果からも、観測波形そのものではなく そこから前の時刻の波群の構造応答を差し引いたものが ソースとなることが分かる。
To confirm this understanding, another calculation was performed. Fig. 3 shows the computation results when only the pulse at \(t=0\) s was given at the borehole station. Fig. 4 shows the corresponding wave field. In this example, the pulse at \(t=1\) s that should appear as a structural response to the pulse at \(t=0\) s is not observed. This absence of the pulse at \(t=1\) s is interpreted as an incidence of a new pulse of negative sign at \(t=1\) s which cancels the positive pulse that should appear. This negative sign pulse propagates the underground from \(t=1\) s to \(t=2\) s, and the same phenomenon is repeat. This result shows that not the observed waveform itself but the waveform subtracted by the structural response of wave packets in the previous times acts as the source.

図3(Fig. 3)


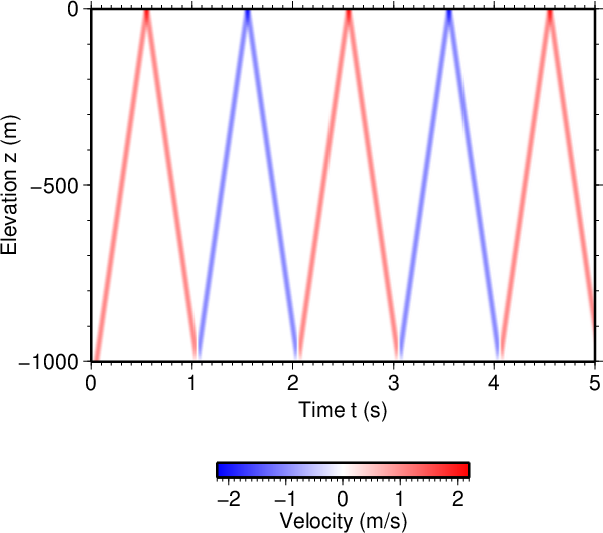
図4(Fig. 4)

以上を踏まえて図1についてもう少し詳しく検討する。 図1bを見ると時刻\(t=1.5\) sから1 s間隔で偽の波群が見られる。 これは恐らく差分法で計算した\(t=0\) sでのパルスの構造応答と、 実際に観測された\(t=1\) sでのパルスとの間に僅かなずれが生じ、 それが新たなソースとなって偽の波群が生成されたと解釈できる。
Based on this interpretation, let us consider more detail on Fig. 1. In Fig. 1b, fake signals are observed at every 1 s after \(t=1.5\) s. This is probably due to a slight difference between the structural response of the pulse at \(t=0\) s computed by the FDM and the actual observed pulse at \(t=1\) s. This slight difference may have acted as a new source to generate the fake signals.
計算した構造応答と観測された\(t=1\) sでのパルスの間にずれが生じた原因としては 差分計算の誤差も考えられるが、 計算に使用した観測波形自体にも本来は無いはずの高周波振動が見られること (図1dの赤線)が一因と思われる。 この高周波振動は観測波形をスペクトルを保ったまま補間する処理によって 生じたものである。 この高周波振動を抑制するため、ローパスフィルターを掛けた波形を用いて 同様のシミュレーションを行ってみた。 観測波形のナイキスト周波数(50 Hz)すれすれの成分が悪さをしたという想像のもと、 (\ref{eq.V.station})(\ref{eq.V.surface})式で表される波形に対して 40 Hz(ゼロ位相、4pole)のローパスフィルターを掛けた。 また、フィルターを掛けるにあたって タイムウインドウの端にシグナルがあるのは好ましくないので 全体を0.5 sだけ遅らせた。
The slight difference between the calculated structural response and the observed pulse at \(t=1\) s may be partially caused by errors in the FDM calculation, but may also be attributed to fake high-frequency oscillations in the observed waveform used (red line in Fig. 1d). These high-frequency oscillations were caused by interpolation of the observed waveform keeping the spectrum. To suppress these oscillations, the same simulation was repeated using a low-pass filtered waveform. Assuming that the frequency contents close to the Nyquist frequency of the observed waveform (50 Hz) caused the high-frequency oscillations, a low-pass filter of 40 Hz (zero phase, 4 poles) was applied to the waveforms of Eqs. (\ref{eq.V.station}) and (\ref{eq.V.surface}). Also all the signals were delayed by 0.5 s to avoid a signal at the edge of the time window which is not good for the low-pass filtering.
このようにして行ったシミュレーションの結果を図5に示す。 期待と異なり、この図5においても補間後の観測波形には高周波振動が残り(図5d)、 計算した地表面での波形にも偽のシグナルが現れる結果となった(図5b)。 このことから補間によって現れる振動には ナイキスト周波数はあまり関係無いと思われる。
The result of this simulation is shown in Fig. 5. Different from the expectation, the high-frequency oscillations remained in the interpolated observed waveform (Fig. 5d), which caused fake signals at the ground surface (Fig. 5b). This suggests that the oscillation caused by the interpolation is not directly related to the Nyquist frequency.

図5(Fig. 5)

そこで次にローパスフィルターのコーナー周波数を20 Hzに下げてみた。 結果を図6に示す。 補間後の観測波形における不規則な振動は抑えられた(図6d)。 なお、この波形におけるパルス前後の規則的な振動は フィルターによって理論的にも出てくるものである。 このように理想的な観測波形が得られたにも関わらず、 計算した地表での波形には偽のシグナルが残ってしまった(図6b)。
Then the corner frequency of the low-pass filter was lowered to 20 Hz. The result is shown in Fig. 6. The irregular oscillations in the interpolated observed waveform were suppressed (Fig. 6d). The regular oscillations before and after the pulse are consistent with the filter response which is also seen in the theoretical waveform. Despite this ideal observed waveform, the calculated waveform at the ground surface still consists of fake signals (Fig. 6b).

図6(Fig. 6)

図7は観測波形の補間が行われないように 最初から差分計算と同じ\(5\times 10^{-4}\) sの時間刻みで 観測波形を作成した場合の結果である。 この場合にはローパスフィルターを掛けずとも 観測波形は理論(青)と計算(赤)で完全に一致する(図7d)。 しかしこの場合であっても地表での計算波形には偽のシグナルが現れる(図7b)。
Fig. 7 shows the results where the interpolation of the observed waveform is completely avoided by creating the original observed waveform at an interval of \(5\times 10^{-4}\) s which is same as the time stepping of the FDM calculation. In this case, the theoretical (blue) and calculated (red) observed waveforms are completely equal without the filtering (Fig. 7d). Nevertheless, fake signals appear in the calculated waveform at the ground surface (Fig. 7b).

図7(Fig. 7)

この図6、図7においては観測点側での偽の振動は抑えられているので、 地表での計算波形における偽のシグナルは差分計算の誤差によって生じたものと思われる。 そこで次に差分計算の刻みを細かくして計算を行ってみた。 まずは差分計算の時間刻み\(\Delta t\)だけをこれまでの計算の1/10 (\(\Delta t=5\times 10^{-5}\) s)にしてみた。 他のパラメータはこれまでと同じである。 20 Hzのローパスフィルターを掛けた場合(図6に相当する計算)の結果を図8に、 観測波形の補間が不要なように差分計算と同じ時間刻みで作成した場合 (図7に相当する計算)の結果を図9に示す。 どちらの場合にも改善は見られなかった。
In Fig. 6 and 7, the fake oscillations in the station side are suppressed, suggesting that the fake signals in the calculated waveform at the ground surface were caused by errors in the FDM calculation. Based on this assumption, finer intervals in the FDM calculation are tested. First, only the time stepping \(\Delta t\) was divided by 10 (i.e., \(\Delta t=5\times 10^{-5}\) s), keeping the other parameters unchanged. Fig. 8 shows the results from low-pass filtering at 20 Hz (corresponding to the case of Fig. 6) and Fig. 9 shows the results from using the observed waveforms with time stepping equal to that of the FDM calculation to avoid interpolation (corresponding to the case of Fig. 7). In both cases, the results did not improve.

図8(Fig. 8)


図9(Fig. 9)

そこで次に\(\Delta z\)についても1/10倍にしてみた。 すなわち\(\Delta t=5\times 10^{-5}\) s、\(\Delta z=0.2\) mであり、 このときには観測点の深さは\(h=1000.1\) mとなる。 この場合の図6, 図7に対応する結果を図10, 図11に示す。 ここでは(b)(d)の縦軸をこれまでの図よりも10倍拡大している点に留意を要する。 この結果から、偽の振動はだいぶ抑えられたことが分かる。
Then \(\Delta z\) was also divided by 10, giving \(\Delta t=5\times 10^{-5}\) s and \(\Delta z=0.2\) m. In this case the station depth is \(h=1000.1\) m. Results for this case corresponding to Fig. 6 and 7 are shown in Fig. 10 and 11, respectively. Note that the vertical axes in (b) and (d) were extended by 10 times the previous figures. Results show that the fake signals were suppresed compared to the previous cases.

図10(Fig. 10)


図11(Fig. 11)

刻みを更に1/10にした場合 (\(\Delta t=5\times 10^{-6}\) s, \(\Delta z=0.02\) m, \(h=1000.01\) m) の結果を図12, 13に示す。 ここでは(b)(d)の縦軸を更に10倍している。 図10, 11に比べて更に偽のシグナルの振幅を小さく抑えられたことが分かる。 なお、この場合であっても計算時間は大してかからない。 著者の環境では2分程度であった。
Results from further dividing the intervals by 10 (i.e., \(\Delta t=5\times 10^{-6}\) s, \(\Delta z=0.02\) m, and \(h=1000.01\) m) are shown in Fig. 12 and 13. Note that the vertical axes in (b) and (d) were additionally multiplied by 10. Compared to Fig. 10 and 11, the amplutudes of the fake signals were further suppressed. The computation time is not so long for this case; it was approximately 2 minutes in the environment of the author.

図12(Fig. 12)


図13(Fig. 13)

以上の結果は以下のように整理できる。
The results above can be summarized as below.


1-2. 時定数0.1秒の様々な関数 (Various functions of 0.1 s time constant)

次に、\(f(t)\)の時定数は\(\tau=0.1\) sに保ったまま 関数形を様々に変えてテストしてみた。 前節の結果を参考に \(\Delta t=5\times 10^{-5}\) s, \(\Delta z=0.2\) m, \(h=1000.1\) m とし、\(f(t)\)には20 Hzのローパスフィルターを掛けた。 これは上記の図10の条件に対応する。
Next, various function forms of \(f(t)\) were tested, keeping the time constant \(\tau=0.1\) s. Based on the summary of the previous section, \(\Delta t=5\times 10^{-5}\) s, \(\Delta z=0.2\) m, and \(h=1000.1\) m were used, and a low-pass filter of 20 Hz was applied to \(f(t)\). This corresponds to the conditions for Fig. 10 above.
まずはガウス関数 \[\begin{equation} f(t)=\exp\left\{-\left[\frac{5(t-\tau)}{\tau}\right]^2\right\} \label{eq.gaussian} \end{equation}\] を用いた場合の結果を図14に示す。 偽のシグナルの形がやや異なるが、 振幅としては図10とほぼ同等の結果が得られた。
Fig. 14 shows results from a Gaussian function (Eq. \ref{eq.gaussian}). Although the shapes of fake signals are different, amplitudes are almost at the same level to those in Fig. 10.

図14(Fig. 14)

pow3-4関数 \[\begin{equation} f(t)= \begin{cases} 0 & (t<0) \\ \left(\frac{7}{3}\right)^3 \left(\frac{7}{4}\right)^4 \left(\frac{t}{\tau}\right)^3 \left(1-\frac{t}{\tau}\right)^4 & (0\leq t\leq \tau) \\ 0 & (\tau<t) \end{cases} \label{eq.pow34} \end{equation}\] を用いた場合の結果を図15に示す。 pow3-4は1周期cos関数に似ているが 2階微分までが連続かつスペクトルホールを持たない最小次数の多項式 としてymaeda_opentoolsの中で考案したものである ( sequence/timefunc.hのマニュアル参照)。 この場合の結果も図14とほぼ同等であった。 2階微分までが連続かつスペクトルホールを持たないという条件が 結果を大きく改善するということは無さそうである。
Results from a pow3-4 function (Eq. \ref{eq.pow34}) is shown in Fig. 15. The pow3-4 function was developed in ymaeda_opentools as the polynominal of minimum possible degrees that satisfies continuity in second order derivative and has no spectral hole, with a similar shape to one-cycle cosine function (see the documentation of sequence/timefunc.h). In this case, the result was similar to Fig. 14. The continuity in second order derivative and no spectral hole seem not significantly improve the result.

図15(Fig. 15)

ricker関数 \[\begin{equation} f(t)=\frac{\sqrt{\pi}}{2}\left[b(t)^2-\frac{1}{2}\right]e^{-b(t)^2} \label{eq.ricker} \end{equation}\] \[\begin{equation} b(t)=\frac{\pi}{\tau}(t-\tau) \label{eq.ricker.b} \end{equation}\] を用いた場合の結果を図16に示す。 これまでに用いてきた関数と異なり、振動する形状であるが、 結果に大差は無い。 結論として関数の形状にはあまり依存しなさそうである。
Result from a ricker function (Eq. \ref{eq.ricker}), where \(b(t)\) is defined by Eq. (\ref{eq.ricker.b}), is shown in Fig. 16. Different from the functions used in the previous examples, the ricker function shows an oscillating shape. However, the result was similar. In conclusion, it seems that the result does not significantly depend on the function shape.

図16(Fig. 16)


1-3. 往復走時よりも長い時定数を用いた場合 (Time constants longer than the round-trip travel time)

これまでは時間関数の時定数が往復走時よりも十分に短い0.1秒の場合を試してきた。 次に時定数が往復走時よりも長い場合を試す。 まずは1周期cos関数(\ref{eq.cos}式)で\(\tau=1.2\) sとした場合の結果を図17に示す。 ここでは(b)(d)の縦軸をこれまでよりも更に大きく引き伸ばしていることに留意する。 この結果から、時定数が長い場合には偽のシグナルが小さくなることが分かる。
So far, 0.1 s was used as the time constant of the time function, which was sufficiently smaller than the round-trip travel time. We next examine the time constants longer than the round-trip travel time. First, result from one-cycle cos function (Eq. \ref{eq.cos}) with \(\tau=1.2\) s is shown in Fig. 17. Here, note that the vertical axis in (b) and (d) are significantly extended from the previous figures. This result shows that the fake signal is small in case of the long time constant.
時定数が長くなることで1波長あたりのグリッド数が増えたためと考えたくなるが、 実はそれだけでは説明がつかない。 \(\tau=0.1\) sの場合に比べて時定数を12倍にしたのであるから 波長は12倍、よって1波長あたりのグリッド数も12倍であり、 1波長あたりのグリッド数だけで考えれば図12の場合とほぼ変わらない。 にも関わらず図12よりも更に偽のシグナルが小さくなっている。
Note that this improvement cannot be explained solely by the numger of grid nodes in a wavelength due to the long time constant. The time constant in this case is 12 times \(\tau=0.1\) s, meaning that the wave length is also 12 times, and thus the number of grid nodes in a wavelength is also 12 times, which is close to the case of Fig. 12. Nevertheless , the fake signal is still smaller than Fig. 12.

図17(Fig. 17)

時定数を更に長く2.4 sにした場合の結果を図18に示す。 直達波と反射波が重なることで偽のシグナルの波形が大きく変化しているが、 偽のシグナルの大きさとしては図17と同程度である。
Result from a longer (2.4 s) time constant is shown in Fig. 18. The waveform of the fake signal significantly changed from the previous case, maybe due to the overlapping of the direct and reflected waves, but the amplitude of the fake signal is similar to that in Fig. 17.

図18(Fig. 18)

時定数\(\tau=1.2\) sのricker関数を用いた場合の結果を図19に示す。 この場合、これまでのテストの中で偽のシグナルは最も小さくなった。
Result from a ricker function with a time constant \(\tau=1.2\) s is shown in Fig. 19. The fake signal is smallest among the tests conducted so far.

図19(Fig. 19)