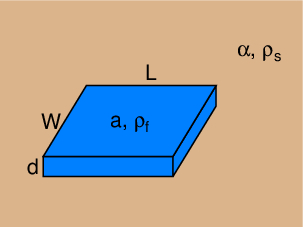
図1. 想定する系の模式図。
Fig. 1. A schematic image for the system assumed.
 図1. 想定する系の模式図。 Fig. 1. A schematic image for the system assumed. |
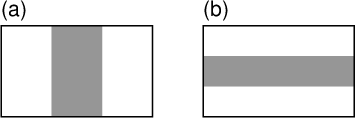 図2. (a)\(L\)モードと(b)\(W\)モードの模式図。 Fig. 2. Schematic images of (a) \(L\)-mode and (b) \(W\)-mode. |
 図3. クラック壁の変位(茶色)と流体圧力擾乱(水色)の振幅の空間分布。 \(x\)は波の伝播方向に沿った位置、 \(L_x\)は波の伝播方向に沿ったクラック長さ(\(L\)または\(W\))を表す。 Maeda and Kumagai (2017)の図8を修正。 Fig. 3. Spatial distributions of the displacement of a crack wall (brown) and the pressure disturbance of fluid (blue); \(x\) and \(L_x\) represent the location and crack length (\(L\) or \(W\)) along the wave propagation direction, respectively. Modified from Fig. 8 of Maeda and Kumagai (2017). |
| パラメータ名 Parameter name |
意味 Meaning |
可能なパラメータ値 Allowed parameter values |
デフォルト値 Default value |
| L | クラックの長さ\(L\) [m]。 The crack length \(L\) [m]. |
正の実数。 A positive real number. |
省略不可 Cannot be omitted |
| W | クラックの幅\(W\) [m]。 The crack width \(W\) [m]. |
正の実数(\(\leq L\))。 A positive real number (\(\leq L\)). |
\(L/2\) |
| d | クラックの厚さ\(d\) [m]。 The crack aperture \(d\) [m]. |
正の実数(\(< W\))。 A positive real number (\(< W\)). |
\(L/10000\) |
| rhof | 流体の密度\(\rho_f\) [kg/m\(^3\)] 。 The density \(\rho_f\) [kg/m\(^3\)] of the fluid. |
正の実数。 A positive real number. |
- |
| rhos | 固体の密度\(\rho_s\) [kg/m\(^3\)]。 The density \(\rho_s\) [kg/m\(^3\)] of the solid. |
正の実数(\(> \rho_f\))。 A positive real number (\(> \rho_f\)). |
- |
| a | 流体の音速\(a\) [m/s]。 The sound velocity \(a\) [m/s] of the fluid. |
正の実数。 A positive real number. |
片方は省略不可、他方は\(\alpha/a=5\)。 One of them cannot be omitted, the other is determined by \(\alpha/a=5\). |
| alpha | 固体のP波速度\(\alpha\) [m/s]。 The P-wave velocity \(\alpha\) [m/s] of the solid. |
正の実数(\(>a\))。 A positive real number (\(> a\)). | |
| ratio_W_L | \(W/L\) | 正の実数(\(<1\))。 A positive real number (\(< 1\)). |
1/2 |
| ratio_L_d | \(L/d\) | 正の実数で、\(W>d\)となるように決める。 A positive real number that must be consistent with \(W>d\). |
10000 |
| ratio_rhof_rhos | \(\rho_f/\rho_s\) | 正の実数(\(<1\))。 A positive real number (\(< 1\)). |
1/120 |
| ratio_alpha_a | \(\alpha/a\) | 正の実数(\(>1\))。 A positive real number (\(> 1\)). |
5 |
| mode | 計算する振動モード(方向)。 The mode (direction) of the oscillation to compute. |
|
L |
| m | 計算するモード次数\(m\)。
クラック癖の変位の波長が\(2L/m\)または\(2W/m\)になるモード
として定義する。 The mode number \(m\) of the ocsillation to compute, defined as an oscillation mode for which the wavelength of the displacement of a crack wall is \(2L/m\) or \(2W/m\). |
整数(\(\geq 2\))。 An integer (\(\geq 2\)). |
省略不可 Cannot be omitted |