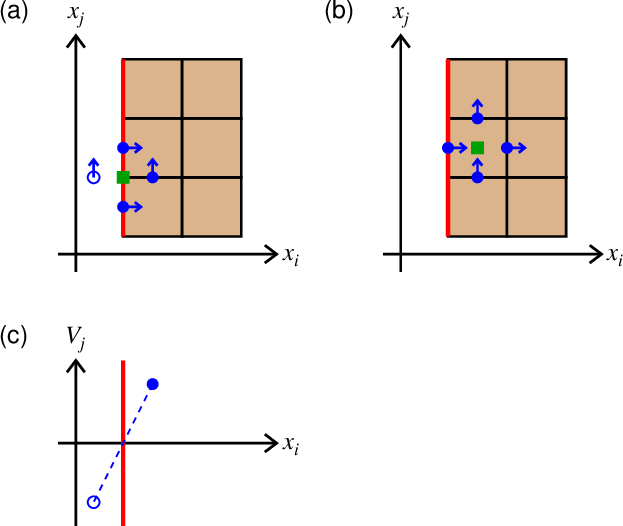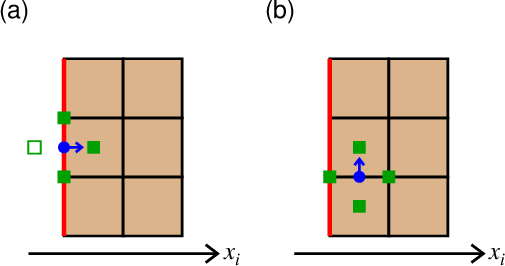
図1. 計算領域端において速度成分を計算する際に発生する問題。 赤線が計算領域端、青が計算したい速度成分、緑が計算に必要な応力成分を表す。 (a)境界面に直交する速度成分を計算する場合。 緑で示した4つの地点での応力成分が必要であるが、 このうち白抜きで示した地点での応力成分が計算領域外なので定義されない。 (b)境界面に平行な速度成分を計算する場合。 このときは問題は起きない。
Fig. 1. A problem for computing velocity components at the outer boundary of the computational volume. The red line is the outer boundary, blue is a velocity component to compute, and green is the stress components needed for the computation. (a) In case of computing a velocity component normal to the boundary. The stress components at the four points shown by green are needed; however, the stress is not defined at the point shown by the open symbol that is out of the computational volume. (b) In case of computing a velocity component parallel to the boundary. In this case, no problem occurs.