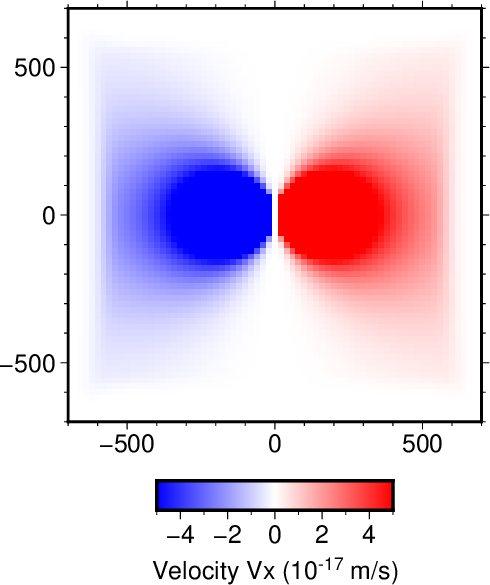
図1. 時刻\(t=1.5\) sでの速度の\(x\)成分\(V_x\)のスナップショット。
Fig. 1. A snapshot of the \(x\)-component velocity \(V_x\) at time \(t=1.5\) s.
| waterPML --Nx=51 --Npmx=10 --x0=-510.0 --y0=-510.0 --z0=-510.0 --dx=20.0 --dt=0.002 --tmax=10.0 --structure_file=structure.ini --structure_file_format=layer --source_file=source.ini --output_dir=result01 --station_file=station_list.dat --snapshot_grid=specify:file=snapshot.ini --snapshot_dt=0.5 |
|
600.0[TAB]2000.0[TAB]1154.7[TAB]2500.0 -1100.0[TAB]2000.0[TAB]1154.7[TAB]2500.0 |
|
newsource dipole location_x=0.0 location_y=0.0 location_z=0.0 mechanism=Mxx intensity=1.0 stfun_name=pow5 stfun_tp=5.0 |
|
station_a[TAB]100.0[TAB]0.0[TAB]0.0 station_b[TAB]200.0[TAB]0.0[TAB]0.0 station_c[TAB]400.0[TAB]0.0[TAB]0.0 station_d[TAB]200.0[TAB]200.0[TAB]0.0 |
|
newsnap z0 snapname z0 xrange -700.0,700.0 yrange -700.0,700.0 zrange -1.0,1.0 |
|
cd result01/snapshot 3d_data_convert z0.Vx.t1.5000 3db 3d |
|
gmt begin z0.Vx.t1.5000 ps gmt set FONT_ANNOT_PRIMARY 12p awk 'BEGIN{ FS="\t" }(NF==4){ print $1,$2,$4*1e+17 }' z0.Vx.t1.5000.3d | gmt xyz2grd -R-700/700/-700/700 -I20/20 -Gz0.Vx.t1.5000.grd gmt makecpt -Cpolar -T-5/5/0.1 -Z -D gmt grdimage z0.Vx.t1.5000.grd -R-700/700/-700/700 -JX7/7 -Xa2 -Ya5 -Bxa500f100 -Bya500f100 -BWSen gmt colorbar -Dx5.5/4/4/0.5h -Bxa2f1 -BS gmt text -R0/21/0/29.7 -JX21/29.7 -Xa0 -Ya0 -F+f12p+jCT <<EOF 5.5 2.7 Velocity Vx (10@+-17@+ m/s) EOF gmt end |
 図1. 時刻\(t=1.5\) sでの速度の\(x\)成分\(V_x\)のスナップショット。 Fig. 1. A snapshot of the \(x\)-component velocity \(V_x\) at time \(t=1.5\) s. |
| WIHM --tmax=10.0 --dt=0.002 --Vp=2000.0 --Vs=1154.7 --rho=2500.0 --source_file=source.ini --station_name=station_b --station_location=200,0,0 --outputfile=result01_WIHM/station_b |
|
cd result01_WIHM sequencefile_convert station_b.Ux seq1 seq2 cd .. |
|
cd result01/waveform sequencefile_integral station_b.Vx.seq1 station_b.Ux.seq2 cd ../.. |
|
mkdir result01_waveform_comparison cd result01_waveform_comparison gmt begin station_b.Ux ps gmt set FONT_ANNOT_PRIMARY 12p awk '(NF==2){ print $1,$2*1e+16 }' ../result01_WIHM/station_b.Ux.seq2 | gmt plot -R0/10/-0.5/7 -JX10/7 -Xa3 -Ya3 -W2,0/127/255 awk '(NF==2){ print $1,$2*1e+16 }' ../result01/waveform/station_b.Ux.seq2 | gmt plot -R0/10/-0.5/7 -JX10/7 -Xa3 -Ya3 -W1,255/0/0 -Bxa2f1 -Bya2f1 -BWSen gmt text -R0/21/0/29.7 -JX21/29.7 -Xa0 -Ya0 -F+f12p+a+j <<EOF 8 2.2 0 CT Time (s) 2.2 6.5 90 CB Displacement (10@+-16@+ m) EOF gmt end |
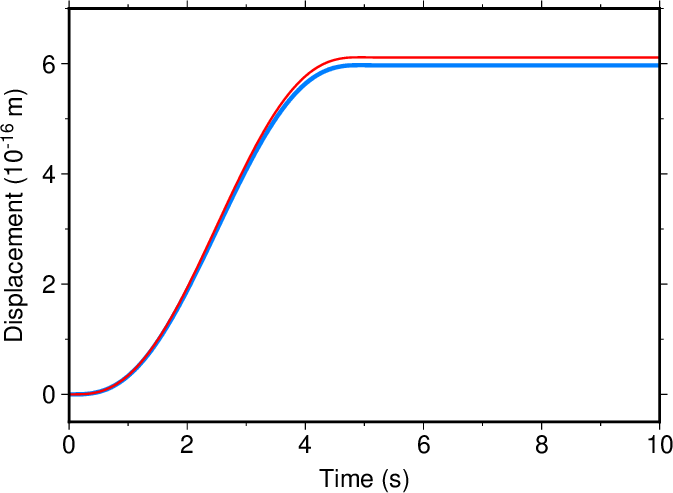 図2. 位置(200,0,0)における\(x\)成分の変位波形。 赤:waterPMLコマンドの結果(数値解)、 青:WIHMコマンドの結果(解析解)。 Fig. 2. Displacement waveforms (\(x\)-component) at a location (200,0,0). Red and blue lines show waterPML (numerical) and WIHM (analytical) solutions, respectively. |