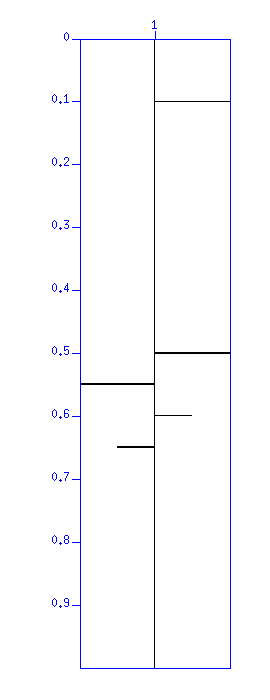
In reflection seismology, a linear model;
Display the reflection coefficient "demo_imp.su".
$ suxwigb < demo_imp.su &

Fig: Reflection coefficients. The vertical axis is 'time (s)'.
Then, create a sweep waveform (wave with increasing or decreasing frequency in time) which is often used by Vibroseis source, and display it.
$ suvibro f1=10 f2=100 tv=1 t1=0.1 t2=0.1 dt=0.001 > tmp_vib.su $ suxwigb < tmp_vib.su &
Display the autocorrelation of the sweep waveform.
$ suacor < tmp_vib.su ntout=201 | suxwigb va=4 & $ suacor < tmp_vib.su ntout=201 sym=0 | suxwigb va=4 &
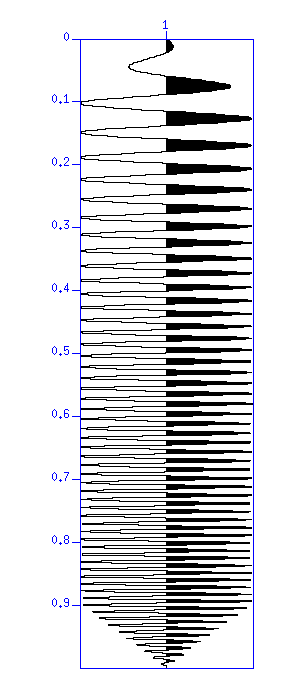
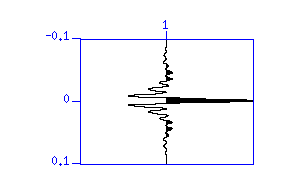
Fig: (Left) Sweep waveform from 10 to 100 Hz. The vertical axis denotes 'time (s)'. (Right) Its auto-correlation. The vertical axis is 'lag time (s)'.
Convolve the reflection coefficient with the sweep waveform, and then add noises. This simulates a seismic wave we usually observe.
$ suconv sufile=tmp_vib.su < demo_imp.su > tmp_cnv.su $ suxwigb < tmp_cnv.su & $ suaddnoise sn=10 < tmp_cnv.su > tmp_cnv_noise.su $ suxwigb < tmp_cnv_noise.su &You can connect the commands with a pipe, so that you can skip the temporary file.
$ suconv sufile=tmp_vib.su < demo_imp.su | suaddnoise sn=10 > tmp_cnv.su $ suxwigb < tmp_cnv.su &
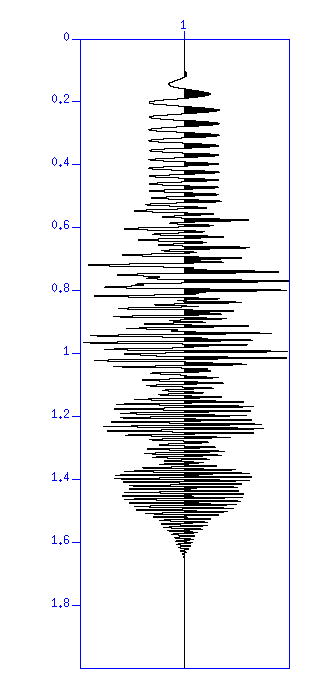
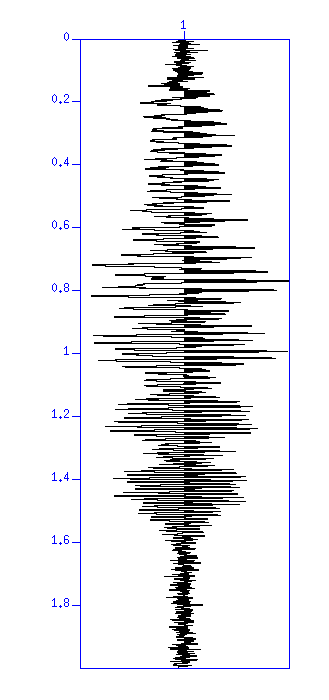
Fig: (Left) Result of convolution without noise. The vertical axis is 'time (s)'. (Right) Waveform after adding noise.
Using Vibroseis source, we observe seismic records like this. Estimating the reflection coefficient from the observed seismic record is our purpose in this chapter.
Calculate cross-correlation of the seismic record and the original sweep wavelet.
$ suxcor sufile=tmp_vib.su < tmp_cnv.su | suxwigb &
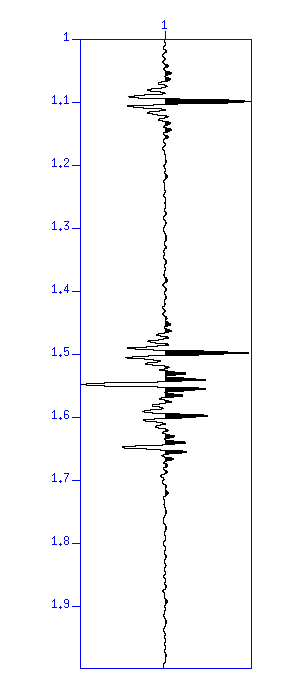

Fig: (Left) Result of cross-correlation. The vertical axis is 'time (s)'. (Right) Original reflection coefficients.
Please recall the assumption that the seismic wave is expressed as;
seismic wave = source wavelet * reflection coefficient + noise
seismic wave (xcor) source wavelet = (source wavelet * reflection coefficient + noise) (xcor) source wavelet = (source wavelet * reflection coefficient) (xcor) source wavelet + noise (xcor) source wavelet => auto-correlation of source wavelet (Clauder Wavelet) * reflection coefficient
First, display the waveform and the autocerrelation of the sample data "demo_dcn.su".
$ suxwigb < demo_dcn.su & $ suacor < demo_dcn.su | sushw key=delrt a=-200 | suxwigb &
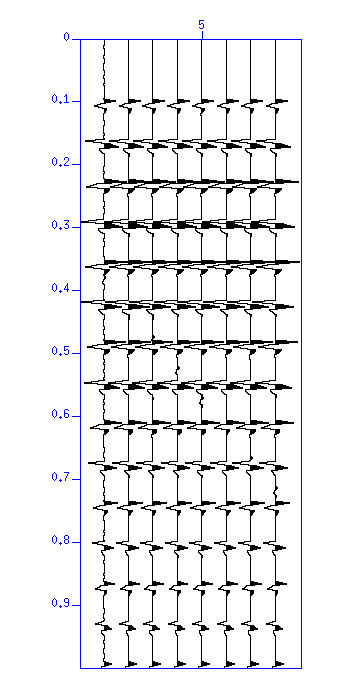
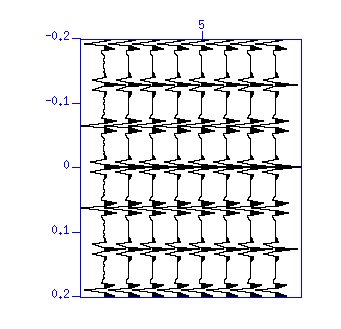
Fig: (Left) Waveform. The vertical axis is 'time (s)'. (Right) Autocorreation. The vertical axis is 'lag time (s)'.
You will see that the repetition with large amplitude is dominant in both the waveforms and the ACFs. You may also notice their polarity is alternating. This is a typical example of multiple reflection in the water (called water reverberations) often seen in the seismic record observed at shallow offshore. They usually mask weak reflections, therefore, it is important to remove these reverberations.
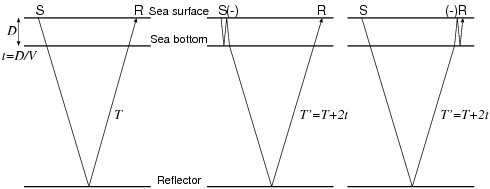
Fig: Illustration of water reverberations.
First, apply a deconvolution filter that converts the wavelet to a pulse (spike), then display the result and its auto-correlation.
$ supef < demo_dcn.su maxlag=???? > tmp_decon.su $ suxwigb < tmp_decon.su & $ suacor < tmp_decon.su | sushw key=delrt a=-200 | suxwigb &
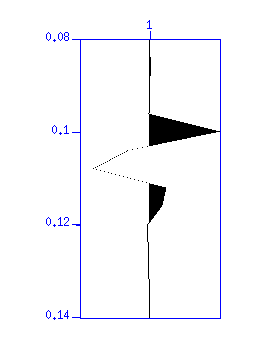
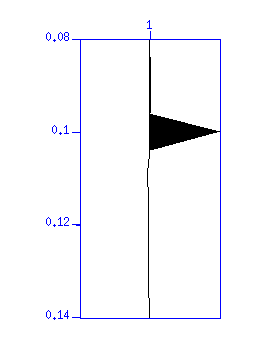
Fig: (Left) Original wavelet (enlargement), (Right) Result of deconvolution.
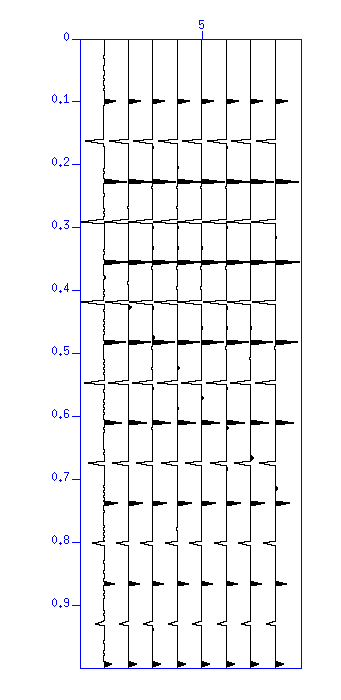
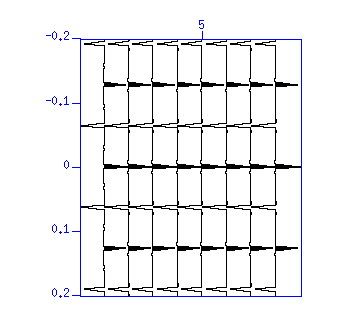
Fig: (Left) Result of deconvolution. The vertical axis is 'time (s)'. (Right) Autocorreation. The vertical axis is 'lag time (s)'. Pulsive autocorrelation shows that the wavelet was converted to a pulse.
Next, apply a PEF that removes the repeated feature in the waveform.
$ supef minlag=???? maxlag=???? < tmp_decon.su | suxwigb & $ supef minlag=???? maxlag=???? < tmp_decon.su | suacor | sushw key=delrt a=-200 | suxwigb &Empirically, these parameters are estimated from the autocorrelation as shown in the figure below. This estimation does not always work. You will need some try-and-errors to find appropriate values.

Try the optimum value for 'minlag' and 'maxlag' using;
If your values are appropriate, the repetition will be removed. A signal indicating dipping layers, which is masked by the water reverberations, will appear as shown in the figures below.
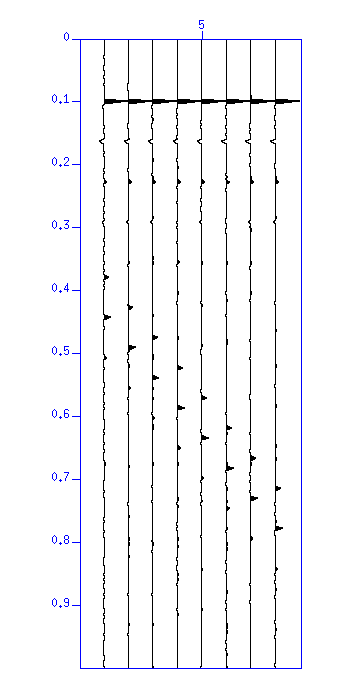
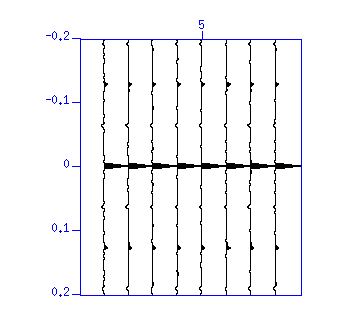
Fig: (Left) Result of deconvolution. The vertical axis is 'time (s)'. (Right) Autocorrelation. The vertical axis is 'lag time (s)'. Autocorrelation also shows that the repetitions are removed.
In usual data processing, a band-pass filter is applied after deconvolution to recover the original spectrum band from the whitened (broadened) spectrum by deconvolution.