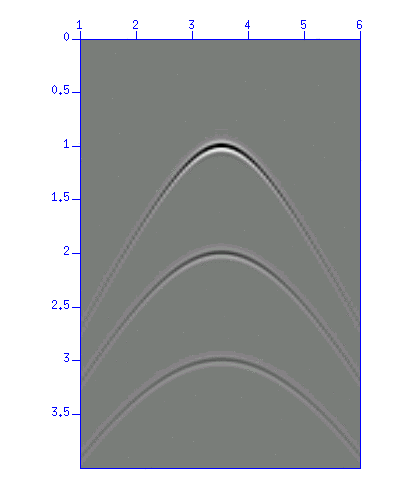
First, display the data "demo_mig1.su".
$ suximage < demo_mig1.su &

Fig: Image display of "demo_mig1.su". The vertical axis is 'time (s)' and the horizontal axis is the CMP number.
This record represents a zero-offset record with three scatterers at different depths.
Check the contents (the range of the header) of the data.
$ surange < demo_mig1.su 101 traces: tracl 1 101 (1 - 101) tracr 1 101 (1 - 101) cdp 1 101 (1 - 101) % CDP from 1 to 101 cdpt 1 trid 1 sx 0 5000 (0 - 5000) gx 0 5000 (0 - 5000) counit 1 ns 201 dt 19999 % dt = 2 (ms), seems strange. d2 0.050000 % CDP interval = 0.05 (km) = 50 (m)We choose "Stolt's migration (Stolt, 1978)", which is an extention of f-k migration, among a lot of migration algorithms. The major reason is its relatively short computation time. Note that migration is usually a time-consuming process.
$ sustolt cdpmin=1 cdpmax=101 tmig=2 vmig=???? dxcdp=50 < demo_mig1.su | suximage &
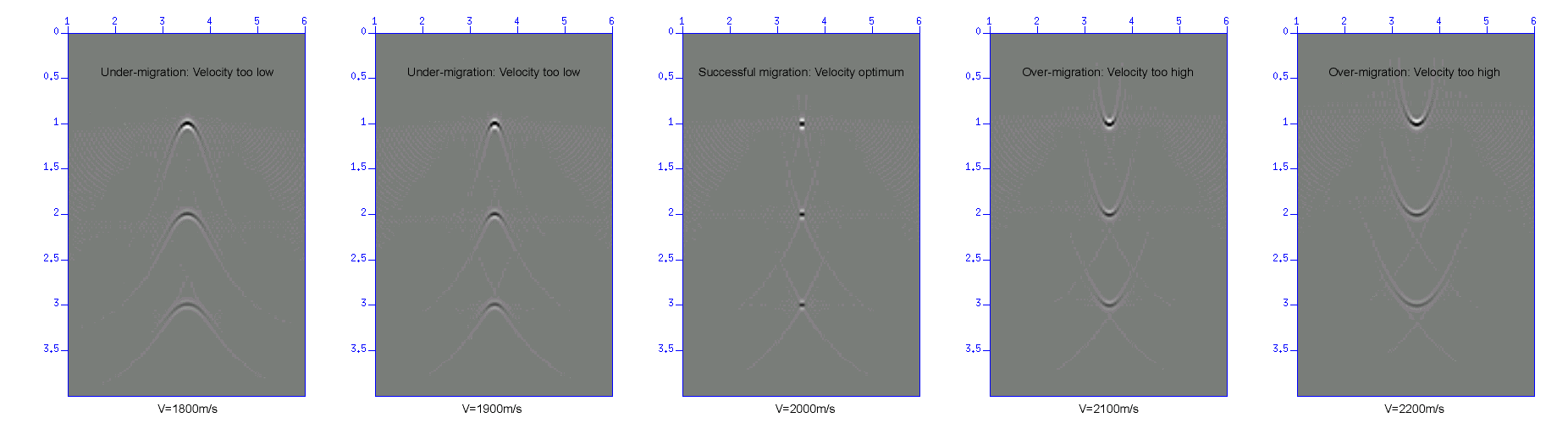
Fig: Migration results obtained using vmig=1800, 1900, 2000, 2100, 2200 (m/s).
From the results, you will see that;
Next, apply the migration to "demo_mig2.su" as well. You need to find the correct velocity value. (Hint: The velocity is constant.) You can do it manually in a try-and error approach. However, it is a clever idea to use the shell script in Exercise 4 after some modifications.


Fig: (Left) Image display of "demo_mig2.su", (Right) migrated result.
You will see that
Next, apply the migration to "demo_mig3.su" as well.
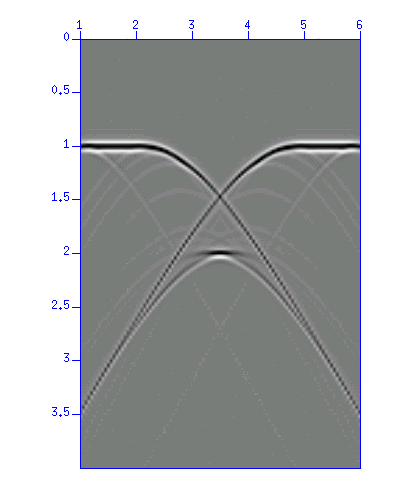
Fig: Image display of "demo_mig3.su".
The velocity is not provided here (it is also constant). Find the appropriate migration velocity, and apply the migration.
Next, apply migration to "demo_mig4.su".
Display "demo_mig4.su".
$ suximage < demo_mig4.su &
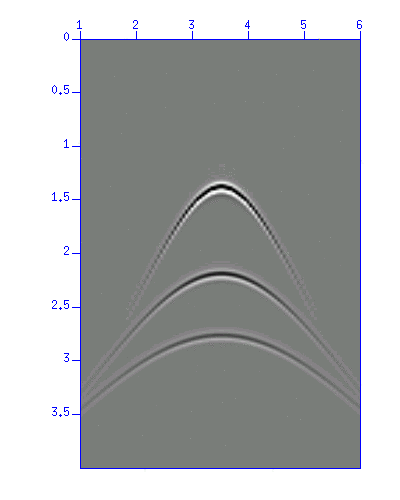
Fig: Image display of "demo_mig4.su".
The image (waveforms) of "demo_mig4.su" looks resemble that of "demo_mig1.su". This record indicates three scatterers at different depths as well as the above example. Apply migration to this record.
$ sustolt cdpmin=1 cdpmax=101 tmig=2 vmig=???? dxcdp=50 < demo_mig4.su | suximage &Try the velocity 'vmig=' from 1400 to 2500 (m/s) and compare the results. It is always a good idea to do this kind of work automatically. you can modify the shell script used in "Exercise 4" and run it.
Now exercising .....
You may have noticed that the three diffractions converge under the different velocity models. This is because the subsurface velocity is no more a constant.
Stolt migration works under 1-D velocity structure, i.e. depth-dependent velocity structure.
$ sustolt cdpmin=1 cdpmax=101 vmig=1400,1500,1600,1700,..... tmig=1.0,1.5,2.0,2.5,..... \ dxcdp=50 < demo_mig4.su | suximage &'\' indicates the continuation of the command line here. You are not supposed to type it.

Fig: An example of the migrated "demo_mig4.su". You will reach this quality of result after some trial-and-errors.