関数points2triangles_rectangular マニュアル

(The documentation of function points2triangles_rectangular)

Last Update: 2023/7/31

◆機能・用途(Purpose)

2次元平面上の点群を用いて三角形要素を構築する(図1a)。その周囲に三角形要素を追加して全体を長方形領域にする(図1b)。
Create triangular elements from points on a 2-D plane (Fig. 1a), and add surrounding triangular elements to make the entire region rectangular (Fig. 1b).

(a)

(b)

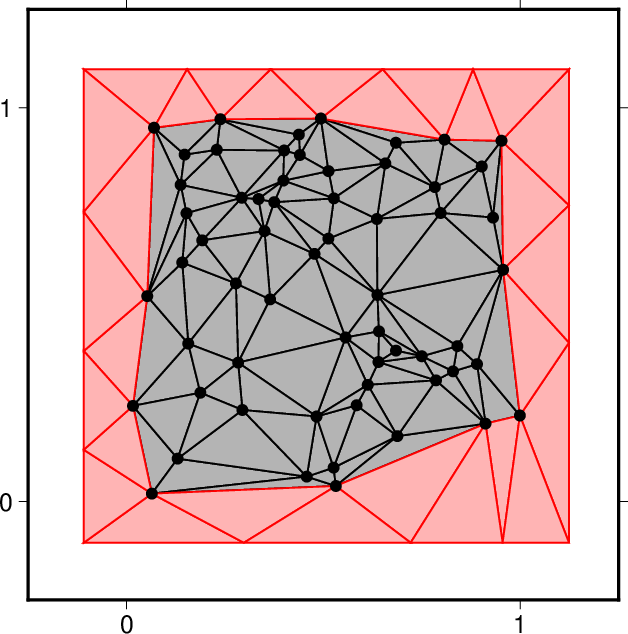
図1. この関数で行うこと。
Fig. 1. Processings done by this function.

◆形式(Format)

#include <geometry.h>
inline int points2triangles_rectangular
(const int Npoints,const double ∗x,const double ∗y,
struct triangle ∗∗triangles,
int ∗Npoints_extended, double ∗∗x_extended,double ∗∗y_extended)

◆引数(Arguments)

Npoints	点の個数。 The number of points.
x	点の\(x\)座標を並べた配列。 An array composed of the \(x\)-coordinates of the points.
y	点の\(y\)座標を並べた配列。 An array composed of the \(y\)-coordinates of the points.
triangles	求めた三角形のリストの代入先。宣言しただけのstruct triangle ∗型変数に&を付けて与える。関数内で配列の動的メモリの確保が行われ、 \(i\)番目の三角形要素の情報がtriangles[i]に代入される。なお、構造体のメンバip1, ip2, ip3, p1, p2, p3のみが設定される。三角形の3つの頂点はip1<ip2<ip3となるように並べられる。 Memory into which the list of triangles is to be inserted. Give an empty struct triangle ∗-type variable with &. Within the function, an array is allocated, and the array components triangles[i] for each \(i\) are set as representing the \(i\)th triangle. Only the members ip1, ip2, ip3, p1, p2, and p3 of the structure are set. The three vertexes of each triangle are sorted as ip1 < ip2 < ip3.
Npoints_extended	外周を含めた点の個数の代入先。元々の点(図1の黒丸)に加え、外周に追加した三角形(図1bの赤)の頂点もカウントに含める。宣言しただけのint型変数に&を付けて与える。 Memory into which the number of points is to be inserted, where both the original points (black dots in Fig. 1) and the vertexes of triangles added outside (red in Fig. 1b) are taken into account. Give an empty int-type variable with &.
x_extended	外周を含めた点の\(x\)座標のリストの代入先。元々の点(図1の黒丸)に加え、外周に追加した三角形(図1bの赤)の頂点もリストに含める。最初に元々の点を引数\(x\)と同じ順番で並べ、次に外周の長方形上の点を南西→南東→北東→北西→南西の順に並べる。宣言しただけのint型変数に&を付けて与える。 Memory into which a list of the \(x\)-coordinates of points is to be inserted, where both the original points (black dots in Fig. 1) and the vertexes of triangles added outside (red in Fig. 1b) are taken into account. The earlier part of this list is simply a copy of argument x, and in the later part, the points on the outer rectangle are sorted as southwest → southeast → northeast → northwest → southwest. Give an empty int-type variable with &.
y_extended	外周を含めた点の\(y\)座標のリストの代入先。元々の点(図1の黒丸)に加え、外周に追加した三角形(図1bの赤)の頂点もリストに含める。最初に元々の点を引数\(y\)と同じ順番で並べ、次に外周の長方形上の点を南西→南東→北東→北西→南西の順に並べる。宣言しただけのint型変数に&を付けて与える。 Memory into which a list of the \(y\)-coordinates of points is to be inserted, where both the original points (black dots in Fig. 1) and the vertexes of triangles added outside (red in Fig. 1b) are taken into account. The earlier part of this list is simply a copy of argument y, and in the later part, the points on the outer rectangle are sorted as southwest → southeast → northeast → northwest → southwest. Give an empty int-type variable with &.

◆戻り値(Return value)

三角形要素の個数。
The number of triangular elements.

◆使用例(Example)

int Npoints=5;
double x[]={1.2,3.4,-5.6,-7.8,9.0};
double y[]={9.8,-7.6,5.4,-3.2,1.0};
int ∗∗triangles;
int Npoints_extended;
double ∗x_extended;
double ∗y_extended;
int Ntriangles=points2triangles_rectangular (Npoints,x,y,&triangles,& Npoints_extended,&x_extended,&y_extended);

◆アルゴリズム(Algorithm)

この関数の処理は

点群を用いて三角形要素を構築する(図1a)
その周囲に三角形要素を追加して全体を長方形領域にする(図1b)

という2つのステップから成る。ステップ1には関数points2triangles が用いられるので、そのアルゴリズムについては同関数のマニュアル参照のこと。ここではステップ2のアルゴリズムについて述べる。
The processings of this function is composed of the following two steps:

creating triangular elements from points (Fig. 1a), and
adding surrounding triangular elements to make the entire region rectangular (Fig. 1b).

The step 1 uses function points2triangles; see the documentation of that function for the algorithm of this step. The description below focuses on the step 2.

●作成する長方形領域 (The rectangular region to create)

ステップ2ではまず最初に目標となる長方形領域を決定する。これには以下のようにする。点の個数を\(N_p\)、点群の\(x\)座標の最小値を\(x_p^{min}\)、最大値を\(x_p^{max}\)、 \(y\)座標の最小値を\(y_p^{min}\)、最大値を\(y_p^{max}\)、とする(図2)。 \[\begin{equation} \Delta\equiv \sqrt{(x_p^{max}-x_p^{min})(y_p^{max}-y_p^{min})/N_p} \label{eq.Delta} \end{equation}\] とおく。大まかに言えば \([x_p^{min},x_p^{max}]\times [y_p^{min},y_p^{max}]\) の領域に\(N_p\)個の点があることになり、 \(N_p\)が十分大きい場合、点1つあたりが専有する面積が\(\Delta^2\)程度、すなわち隣接する点と点の平均的な間隔が\(\Delta\)程度であると見なせる。この\(\Delta\)を用いて \([x_p^{min}-\Delta,x_p^{max}+\Delta] \times [y_p^{min}-\Delta,y_p^{max}+\Delta]\) を目標の長方形領域とする(図2)。
In the step 2, the target rectangular region is first determined as follows. Let \(N_p\) be the number of points, \(x_p^{min}\) and \(x_p^{max}\) be the minimum and maximum values of the \(x\)-coordinates of the points, respectively, and \(y_p^{min}\) and \(y_p^{max}\) be those of the \(y\)-coordinates (Fig. 2). Let \(\Delta\) be defined by Eq. (\ref{eq.Delta}). Roughly, the \(N_p\) points are distributed in the region \([x_p^{min},x_p^{max}]\times [y_p^{min},y_p^{max}]\). When \(N_p\) is large enough, each point occupies an area of \(\sim \Delta^2\), and thus average distance between adjacent points is approximately \(\Delta\). Using this \(\Delta\), \([x_p^{min}-\Delta,x_p^{max}+\Delta] \times [y_p^{min}-\Delta,y_p^{max}+\Delta]\) is the target rectangular region (Fig. 2).

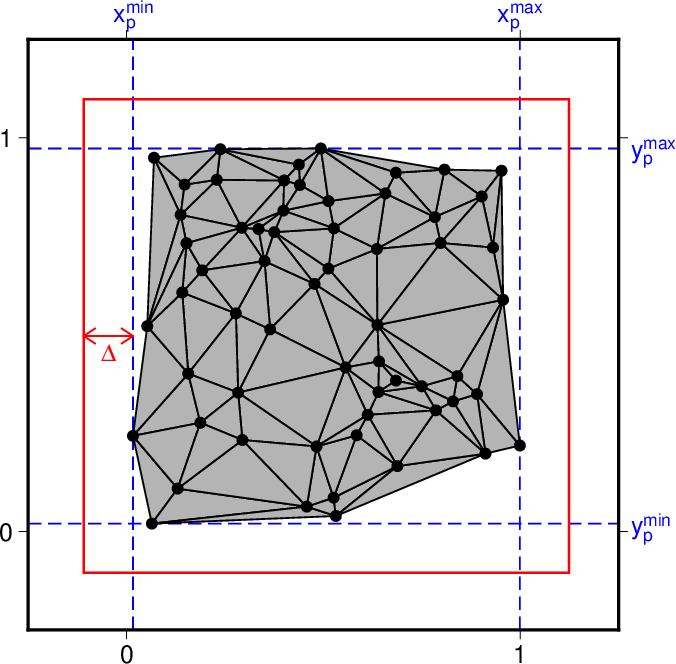図2. 目標とする長方形(赤)。
Fig. 2. The target rectangle to create (red).

●外周の辺の抽出と並べ替え (Listing and sorting the edges on the outer bounds)

点群を用いて三角形要素を構築した場合、それらの要素は隙間なく重複なく1つの閉領域を形成することになる(図1a)。このとき、三角形の辺のうち領域内部に位置するものは2つの三角形で共有され、領域外周に位置するものは1つの三角形のみの辺である。この性質を用いて領域外周に位置する辺をリストアップする(図3)。
The triangular elements created from points constitute a closed region without gaps nor overlaps (Fig. 1a). Each edge of a triangle is shared by two triangles if it is in the region, while the edge is occupied by a single triangle if it is on the boundary of the region. Using this difference, edges on the outer boundary of the region are listed (Fig. 3).

領域外周の辺は全体として1つの閉曲線をなすのであるから(図3)、辺は分岐したり途切れたりせず、 1つの辺の終点が次の辺の始点になるように辺の順番を並べ替えることができる。このように並べ替えることで、辺は領域の外周に沿って時計回りまたは反時計回りに1周する順番となる。
Because the edges on the outer boundary constitute a closed line (Fig. 3), they do not brunch nor terminate, and their order can be sorted such that the end of one edge is the start of the next edge. After this sorting, the edges go around the outer boundary, either clockwise or counterclockwise.

図3. 領域外周に位置する辺(赤)。
Fig. 3. The edges located on the outer boundary (red).

●領域からの方位による外周の辺の区間分割 (Division to sections for the outer edges based on the directions from the region)

上でリストアップした領域外周を構成する点の中で、長方形の南西端\((x_p^{min}-\Delta,y_p^{min}-\Delta)\) の最寄りの点を\((x_p^{sw},y_p^{sw})\)、長方形の南東端\((x_p^{max}+\Delta,y_p^{min}-\Delta)\) の最寄りの点を\((x_p^{se},y_p^{se})\)、長方形の北東端\((x_p^{max}+\Delta,y_p^{max}+\Delta)\) の最寄りの点を\((x_p^{ne},y_p^{ne})\)、長方形の北西端\((x_p^{min}-\Delta,y_p^{max}+\Delta)\) の最寄りの点を\((x_p^{nw},y_p^{nw})\) とする。上でリストアップ・並べ替えした領域外周の辺を

南区間: \(x_p^{sw},y_p^{sw}\)から\(x_p^{se},y_p^{se}\)までの区間
東区間: \(x_p^{se},y_p^{se}\)から\(x_p^{ne},y_p^{ne}\)までの区間
北区間: \(x_p^{ne},y_p^{ne}\)から\(x_p^{nw},y_p^{nw}\)までの区間
西区間: \(x_p^{nw},y_p^{nw}\)から\(x_p^{sw},y_p^{sw}\)までの区間

に分割する(図4)。
Let \((x_p^{sw},y_p^{sw})\), \((x_p^{se},y_p^{se})\), \((x_p^{ne},y_p^{ne})\), and \((x_p^{nw},y_p^{nw})\) be the points on the outer boundary of the region listed above closest to the southwestern corner \((x_p^{min}-\Delta,y_p^{min}-\Delta)\), southeastern corner \((x_p^{max}+\Delta,y_p^{min}-\Delta)\), northeastern corner \((x_p^{max}+\Delta,y_p^{max}+\Delta)\), and northwestern corner \((x_p^{min}-\Delta,y_p^{max}+\Delta)\) of the target rectangle, respectively. Divide the outer edges of the boundary listed and sorted in the previous step into the following four sections (Fig. 4):

southern section from \(x_p^{sw},y_p^{sw}\) to \(x_p^{se},y_p^{se}\),
eastern section from \(x_p^{se},y_p^{se}\) to \(x_p^{ne},y_p^{ne}\),
northern section from \(x_p^{ne},y_p^{ne}\) to \(x_p^{nw},y_p^{nw}\), and
western section from \(x_p^{nw},y_p^{nw}\) to \(x_p^{sw},y_p^{sw}\).

図4. 領域外周に位置する辺の区間による分割。赤:南区間。緑:東区間。青:北区間。紫:西区間。
Fig. 4. Division of the edges located on the outer boundary to sections. Red, green, blue, and purple are the southern, eastern, northern, and western sections, respectively.

●領域南側の三角形要素の構築 (Creating the triangular elements to the southern side)

南区間を構成する辺の頂点を順に \((x_0^s,y_0^s), (x_1^s,y_1^s), (x_2^s,y_2^s), \cdots, (x_N^s,y_N^s)\) とする。但し\((x_0^s,y_0^s)=(x_p^{sw},y_p^{sw})\), \((x_N^s,y_N^s)=(x_p^{se},y_p^{se})\) であるものとする(図5)。
Let the points on the edges in the southern section be \((x_0^s,y_0^s), (x_1^s,y_1^s), (x_2^s,y_2^s), \cdots, (x_N^s,y_N^s)\), where \((x_0^s,y_0^s)=(x_p^{sw},y_p^{sw})\) and \((x_N^s,y_N^s)=(x_p^{se},y_p^{se})\) (Fig. 5).

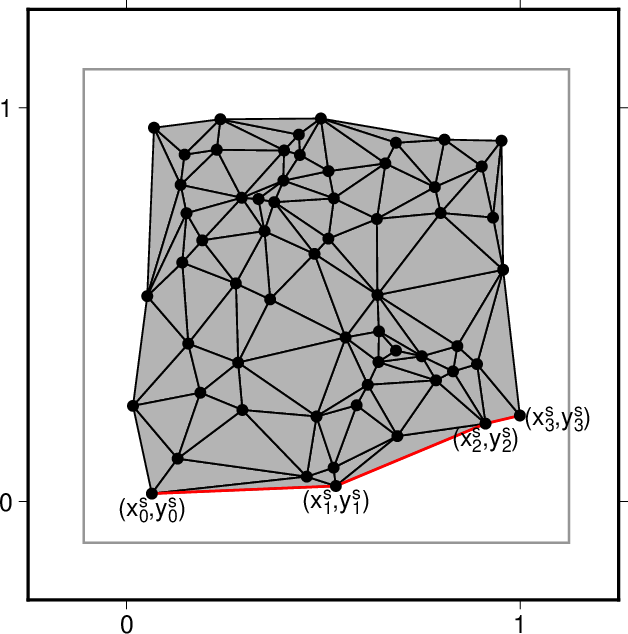図5. 南区間の点の番号付け。
Fig. 5. Renumbering of the points on the southern section.

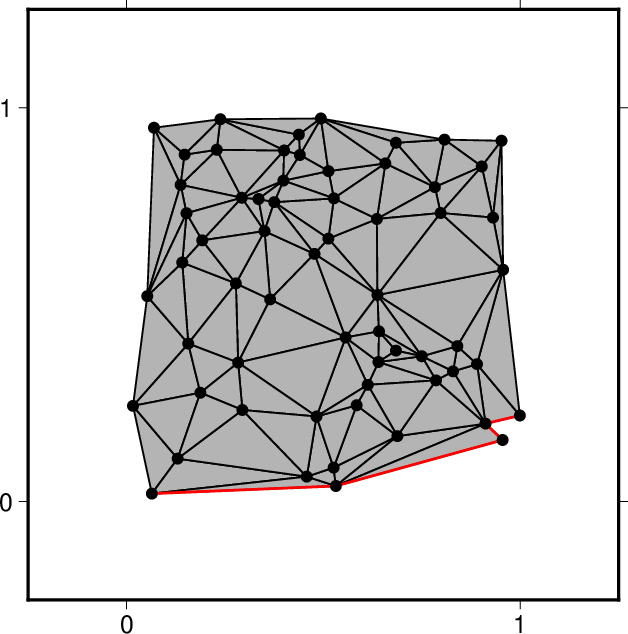この関数では \(x_0^s<x_1^s<x_s^2<\cdots <x_N^s\) であることを必要とする。この条件が成り立っていない場合(例えば図6のようなケース)はプログラムをエラー終了する。
This function requires \(x_0^s<x_1^s<x_s^2<\cdots <x_N^s\). If this requirement is not satisfied (for example the case of Fig. 6), the program finishes as an error.

図6. \(x_0^s<x_1^s<x_s^2<\cdots <x_N^s\) が成り立たないケース。この場合はエラー終了する。
Fig. 6. A case where \(x_0^s<x_1^s<x_s^2<\cdots <x_N^s\) does not hold. In this case, the program finishes as an error.

上記の条件が成り立っているものとして、南区間の点と、南区間の辺の中点の真南の長方形上の点を結んで三角形要素を構築する(図7)。明示的に書くと、構築するのは以下の4種類の三角形である。

長方形の南西端\((x_p^{min}-\Delta,y_p^{min}-\Delta)\)、その最寄りの点\((x_p^{sw},y_p^{sw})(=(x_0^s,y_0^s))\)、点\(((x_0^s+x_1^s)/2,y_p^{min}-\Delta)\) を結んだ三角形(図7緑)。
3点\((x_i^s,y_i^s)\)、\((x_{i+1}^s,y_{i+1}^s)\)、 \(((x_i^s+x_{i+1}^s)/2,y_p^{min}-\Delta)\) (\(i=0,1,2,\cdots,N-1\))を結んだ三角形(図7赤)。
3点\((x_i^s,y_i^s)\)、 \(((x_{i-1}^s+x_i^s)/2,y_p^{min}-\Delta)\)、 \(((x_i^s+x_{i+1}^s)/2,y_p^{min}-\Delta)\) (\(i=1,2,\cdots,N-1\))を結んだ三角形(図7青)。
長方形の南東端\((x_p^{max}+\Delta,y_p^{min}-\Delta)\)、その最寄りの点\((x_p^{se},y_p^{se})(=(x_N^s,y_N^s)\)、点\(((x_{N-1}^s+x_N^s)/2,y_p^{min}-\Delta)\) を結んだ三角形(図7紫)。

Suppose that the requirement mentioned above is satisfied. Create triangular elements by connecting the points on the southern section and the mid-points of the edges on the section projected onto the southern edge of the rectangle (Fig. 7). Explicitly, this involves the following four types of triangles:

a triangle created by connecting the southwestern corner of the rectangle \((x_p^{min}-\Delta,y_p^{min}-\Delta)\), its nearest point \((x_p^{sw},y_p^{sw})(=(x_0^s,y_0^s))\), and a point \(((x_0^s+x_1^s)/2,y_p^{min}-\Delta)\) (green in Fig. 7);
triangles created by connecting the points \((x_i^s,y_i^s)\), \((x_{i+1}^s,y_{i+1}^s)\), and \(((x_i^s+x_{i+1}^s)/2,y_p^{min}-\Delta)\), where \(i=0,1,2,\cdots,N-1\) (red in Fig. 7);
triangles created by connecting the points \((x_i^s,y_i^s)\), \(((x_{i-1}^s+x_i^s)/2,y_p^{min}-\Delta)\), and \(((x_i^s+x_{i+1}^s)/2,y_p^{min}-\Delta)\), where \(i=1,2,\cdots,N-1\) (blue in Fig. 7); and
a triangle created by connecting the southeastern corner of the rectangle \((x_p^{max}+\Delta,y_p^{min}-\Delta)\), its nearest point \((x_p^{se},y_p^{se})(=(x_N^s,y_N^s)\), and a point \(((x_{N-1}^s+x_N^s)/2,y_p^{min}-\Delta)\) (purple in Fig. 7).

図7. 南区間の外側に作成する4種類の三角形。
Fig. 7. Four types of triangles added to the southern side.

●領域東側、北側、西側の三角形要素の構築 (Creating the triangular elements to the eastern, northern, and western sides)

領域東側、北側、西側の三角形要素は領域南側と同じ要領で構築する。
Create the triangular elements to the eastern, northern, and western sides in the same manner as those to the southern side.

◆補足(Additional notes)

この関数では引数x, yで与えられた順番で点を選んでいく。点をランダムな順番で選択したい場合には関数の外で予めx, yの配列要素の並べ替え(乱数順)を行っておくこと。
This function choose the points in the order of arguments x and y. To choose the points with a randomized order, randomly sort the array components of x and y outside the function in advance to the function call.
点の個数が多い場合、処理に時間がかかることがある。マクロPOINTS2TRIANGLES_VERBOSEを定義しておくことで関数内での処理の進行状況を表示できる。
The processings of this function may take time depending on the number of points. The function displays the progress if a macro POINTS2TRIANGLES_VERBOSE is defined.