図1(Fig. 1)
 図1(Fig. 1) |
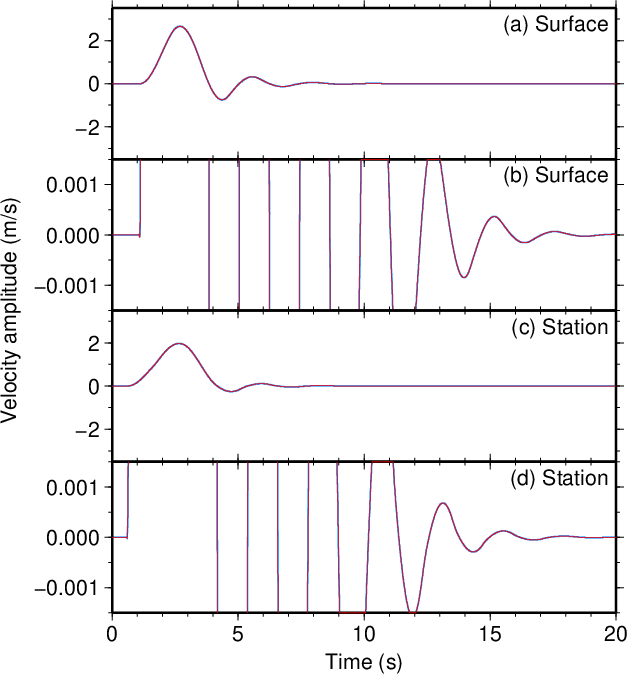 図2(Fig. 2) |
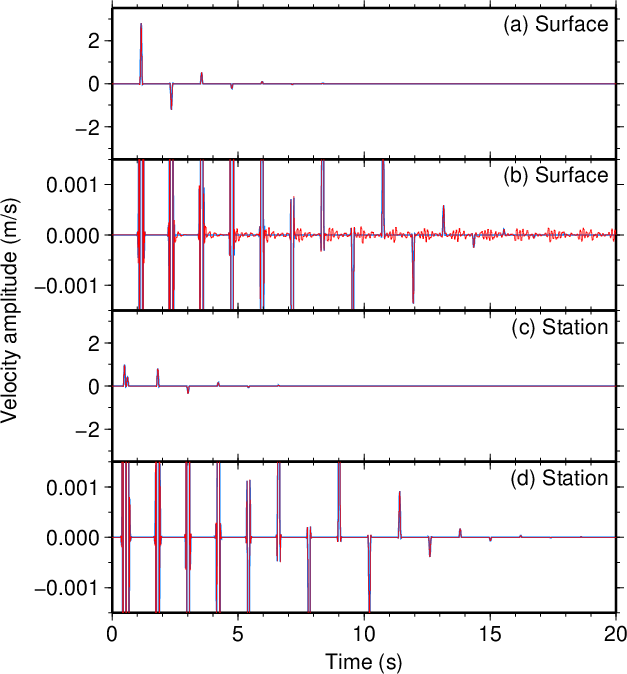 図3(Fig. 3) |
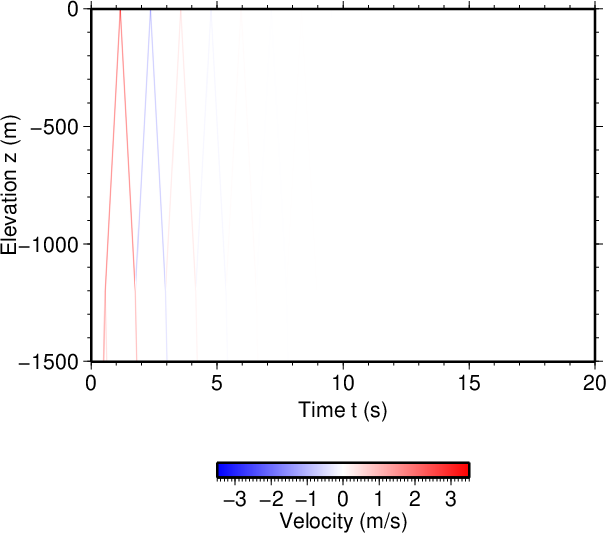 図4(Fig. 4) |
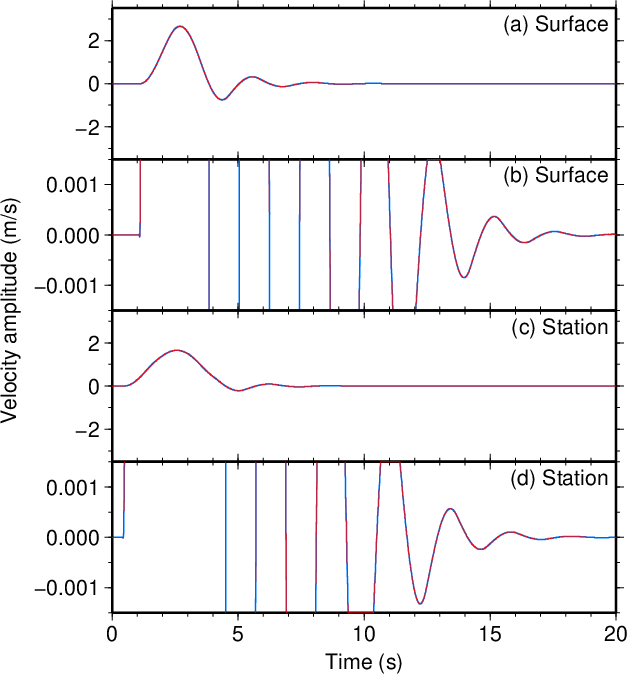 図5(Fig. 5) |
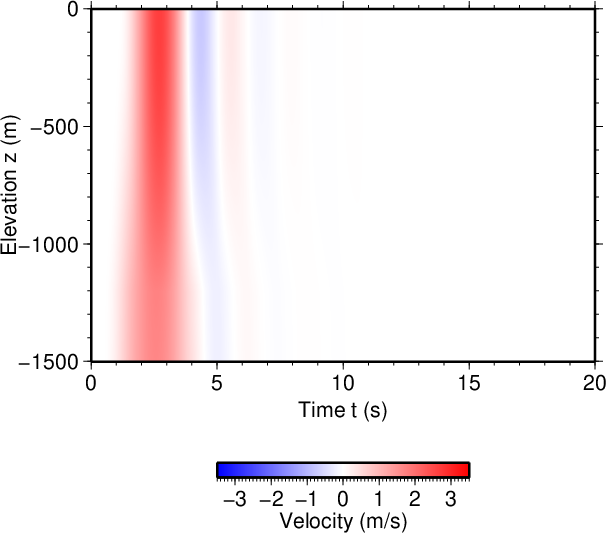 図6(Fig. 6) |
表1 (Table 1)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
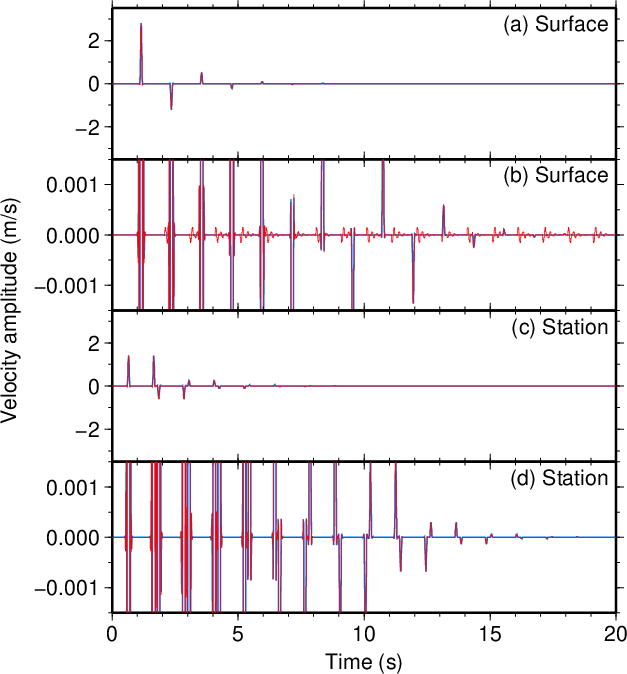
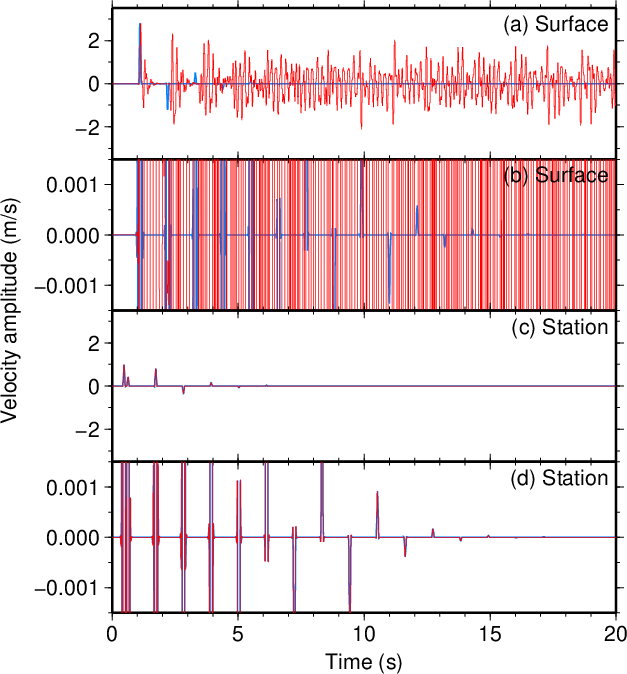 図7. \(d\)が100 mだけ小さい場合(\(\tau=0.1\) s)。 Fig. 7. Decreased \(d\) by 100 m (\(\tau=0.1\) s). |
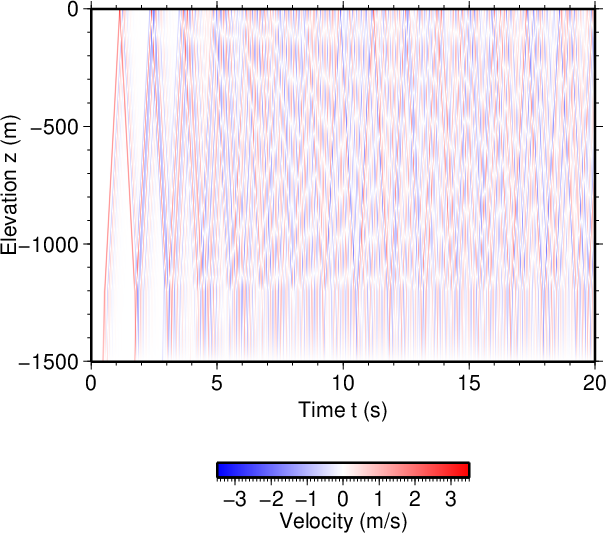 図8. \(d\)が100 mだけ小さい場合(\(\tau=0.1\) s)。 Fig. 8. Decreased \(d\) by 100 m (\(\tau=0.1\) s). |
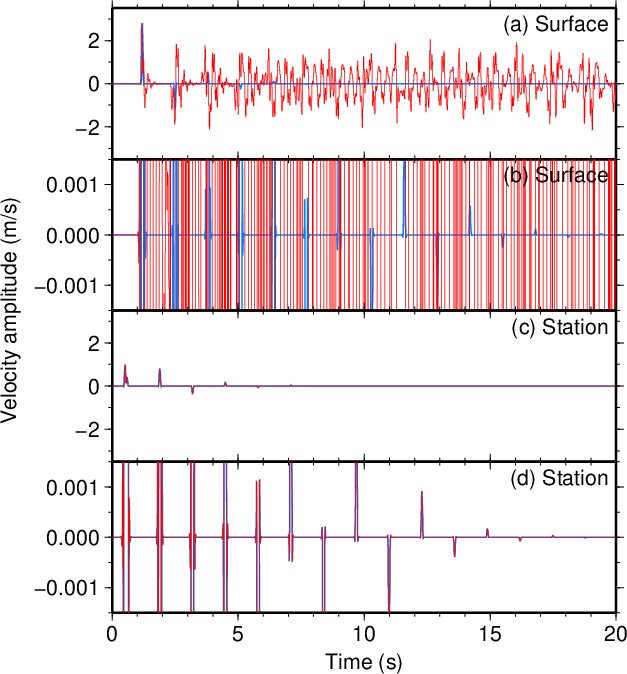 図9. \(d\)が100 mだけ大きい場合(\(\tau=0.1\) s)。 Fig. 9. Increased \(d\) by 100 m (\(\tau=0.1\) s). |
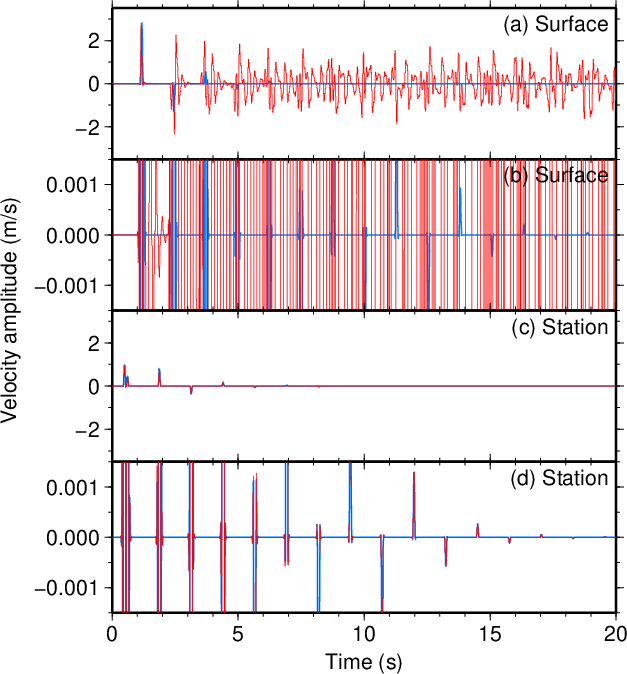 図10. \(V_1\)が100 m/sだけ小さい場合(\(\tau=0.1\) s)。 Fig. 10. Decreased \(V_1\) by 100 m/s (\(\tau=0.1\) s). |
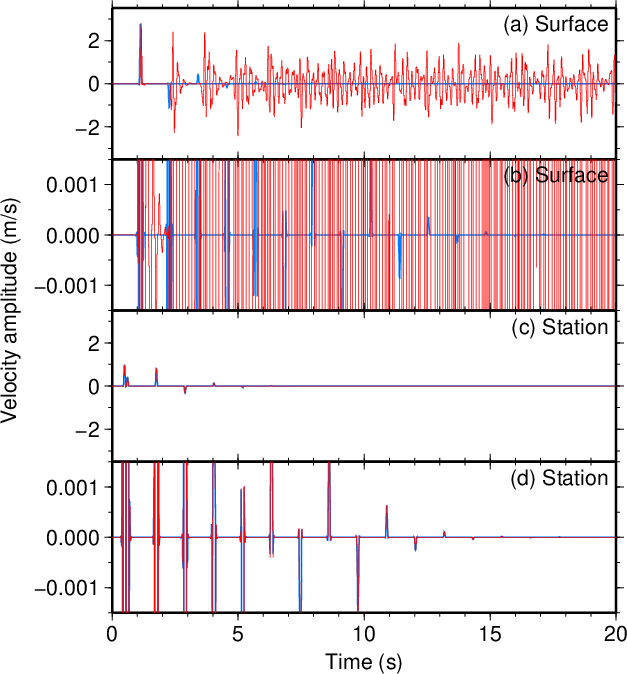 図11. \(V_1\)が100 m/sだけ大きい場合(\(\tau=0.1\) s)。 Fig. 11. Increased \(V_1\) by 100 m/s (\(\tau=0.1\) s). |
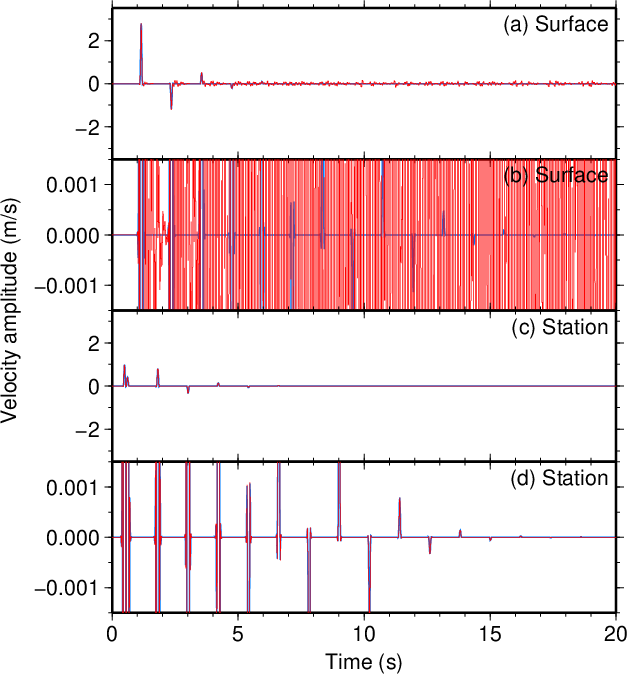 図12. \(V_2\)が100 m/sだけ小さい場合(\(\tau=0.1\) s)。 Fig. 12. Decreased \(V_2\) by 100 m/s (\(\tau=0.1\) s). |
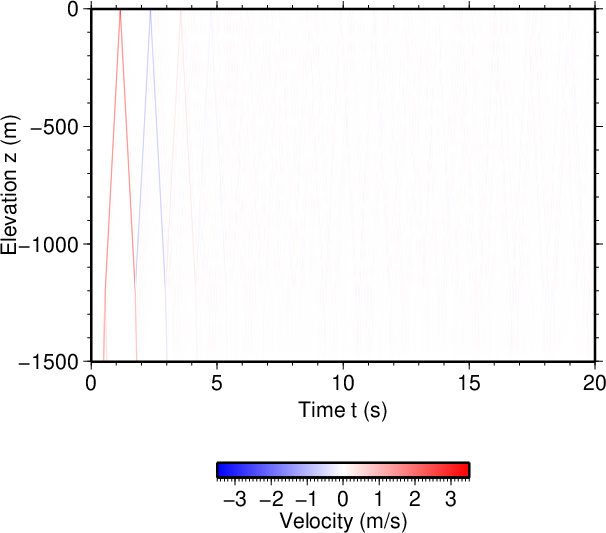 図13. \(V_2\)が100 m/sだけ小さい場合(\(\tau=0.1\) s)。 Fig. 13. Decreased \(V_2\) by 100 m/s (\(\tau=0.1\) s). |
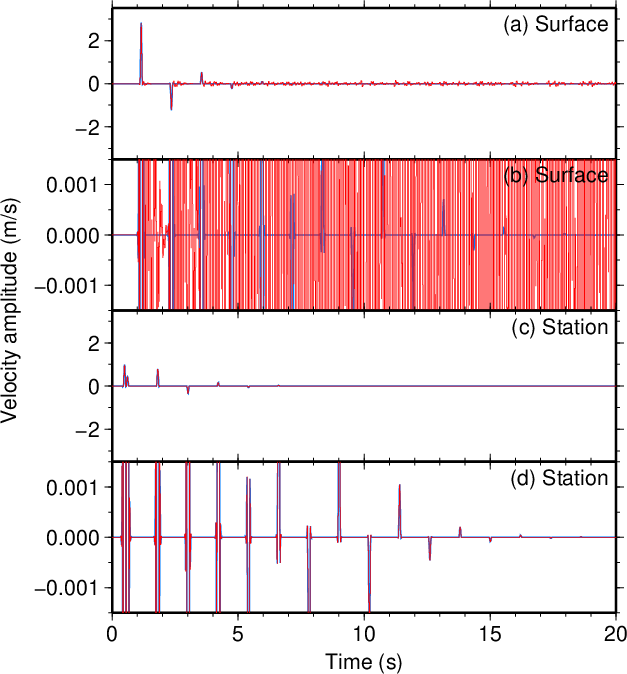 図14. \(V_2\)が100 m/sだけ大きい場合(\(\tau=0.1\) s)。 Fig. 14. Increased \(V_2\) by 100 m/s (\(\tau=0.1\) s). |
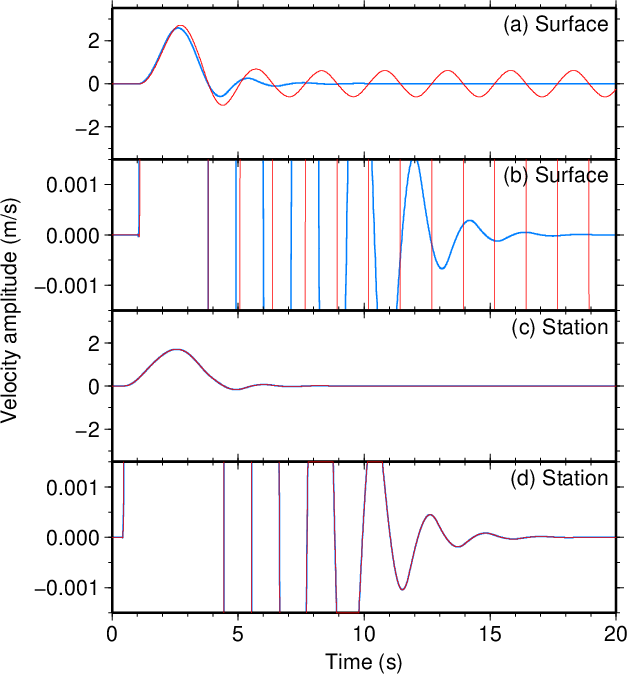 図15. \(d\)が100 mだけ小さい場合(\(\tau=3.5\) s)。 Fig. 15. Decreased \(d\) by 100 m (\(\tau=3.5\) s). |
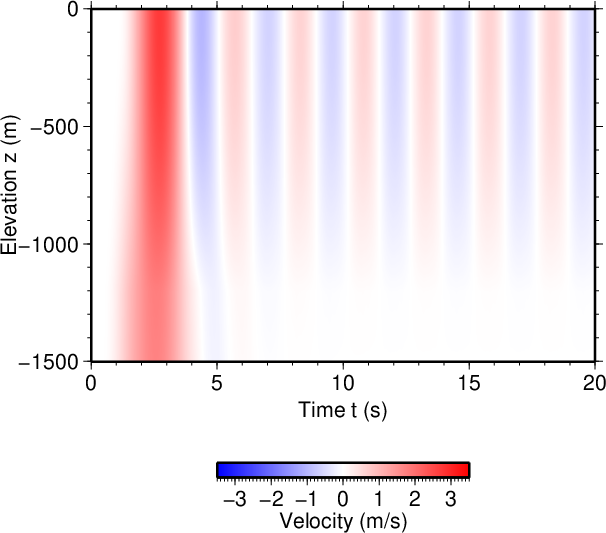 図16. \(d\)が100 mだけ小さい場合(\(\tau=3.5\) s)。 Fig. 16. Decreased \(d\) by 100 m (\(\tau=3.5\) s). |
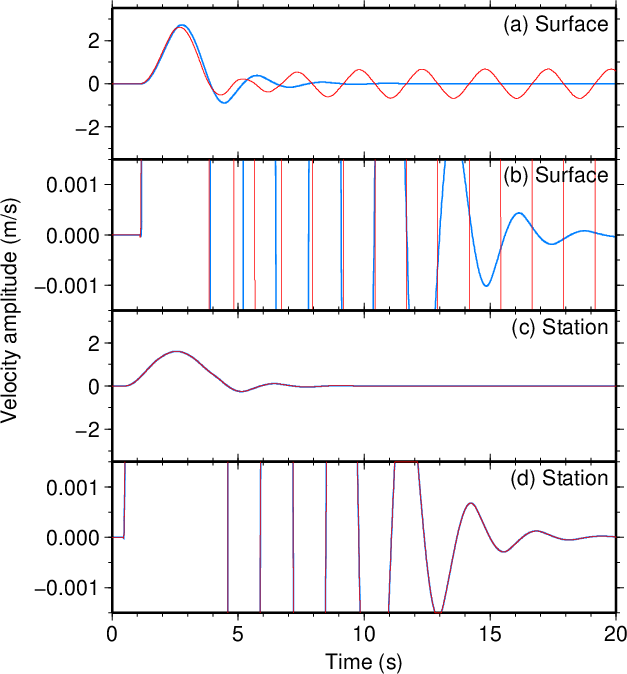 図17. \(d\)が100 mだけ大きい場合(\(\tau=3.5\) s)。 Fig. 17. Increased \(d\) by 100 m (\(\tau=3.5\) s). |
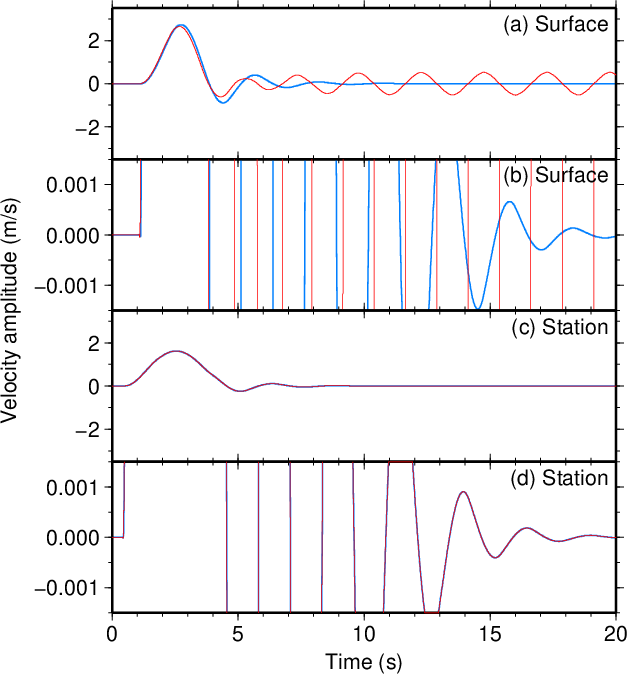 図18. \(V_1\)が100 m/sだけ小さい場合(\(\tau=3.5\) s)。 Fig. 18. Decreased \(V_1\) by 100 m/s (\(\tau=3.5\) s). |
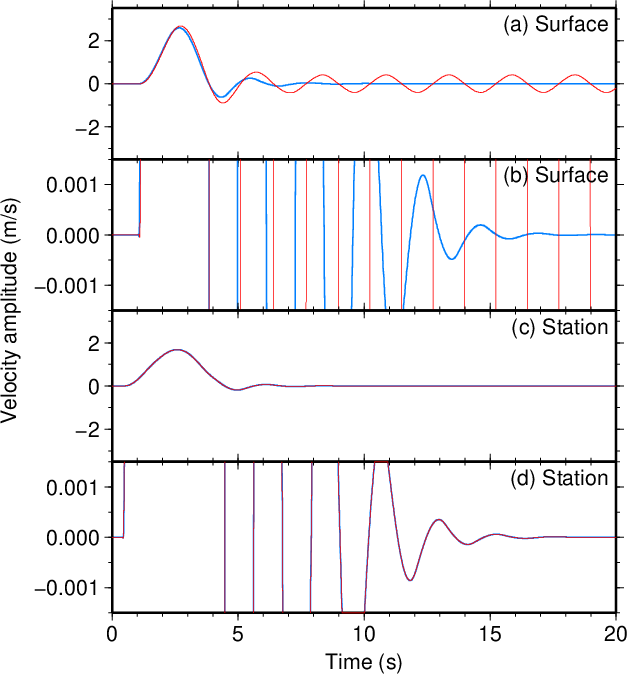 図19. \(V_1\)が100 m/sだけ大きい場合(\(\tau=3.5\) s)。 Fig. 19. Increased \(V_1\) by 100 m/s (\(\tau=3.5\) s). |
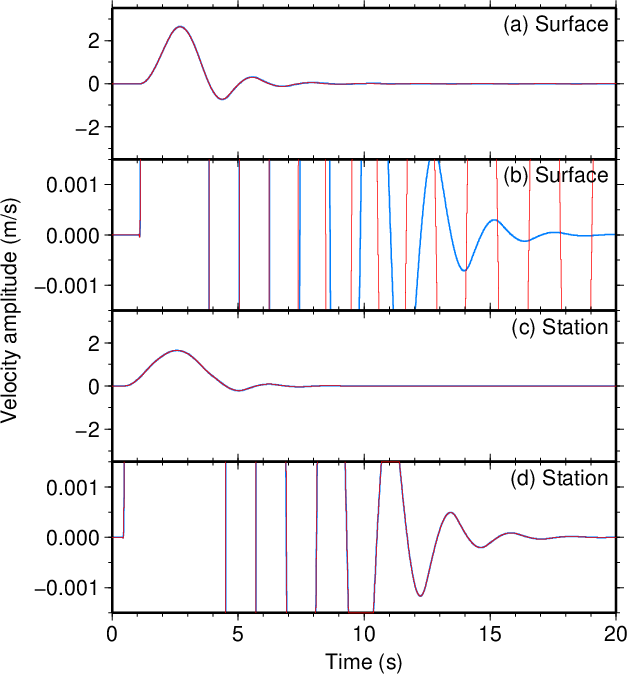 図20. \(V_2\)が100 m/sだけ小さい場合(\(\tau=3.5\) s)。 Fig. 20. Decreased \(V_2\) by 100 m/s (\(\tau=3.5\) s). |
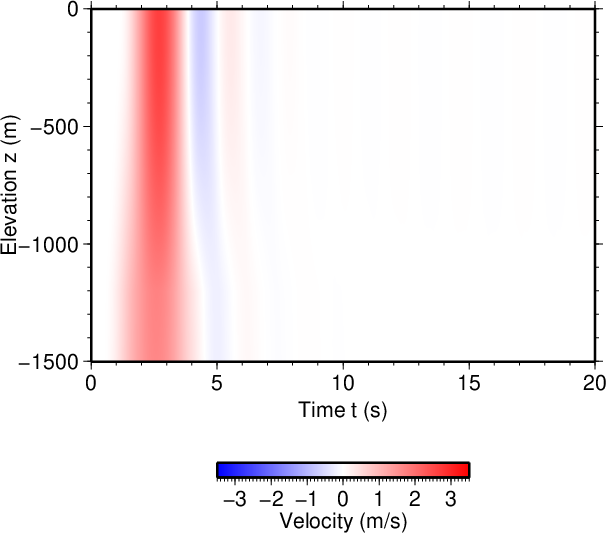 図21. \(V_2\)が100 m/sだけ小さい場合(\(\tau=3.5\) s)。 Fig. 21. Decreased \(V_2\) by 100 m/s (\(\tau=3.5\) s). |
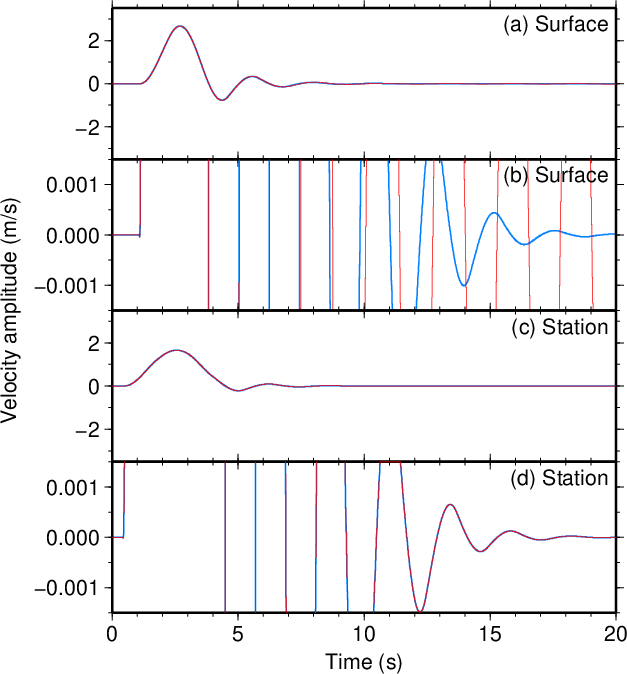 図22. \(V_2\)が100 m/sだけ大きい場合(\(\tau=3.5\) s)。 Fig. 22. Increased \(V_2\) by 100 m/s (\(\tau=3.5\) s). |