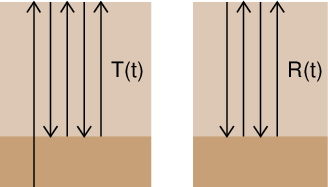
図1. このプログラムで考える地震波伝播の模式図。
Fig. 1. A schematic image for the seismic wave propagation assumed in this program.
 図1. このプログラムで考える地震波伝播の模式図。 Fig. 1. A schematic image for the seismic wave propagation assumed in this program. |
| パラメータ名 Parameter name |
意味 Meaning |
可能なパラメータ値 Allowed parameter values |
デフォルト値 Default value |
| datadir | 観測に用いる地震波形が保存されているディレクトリパス。 A directory path in which the seismograms to use are stored.
|
ディレクトリ名を表す文字列。 A string that represents a directory name. |
省略不可 Cannot be omitted |
| traveltime_list_file | 各イベント・各観測点の波形における
イベントの信号の到着時刻のリストファイル
(走時リストファイル)名。 The name of a file in which the arrival time of the event signal in the waveform for each event and station are listed (traveltime list file). このファイルには1行につき1つの到着時刻を書く。 各行は3列から成り、
In this file, write information for an arrival time in each line, composed of the following three columns:
第3列の値(イベント信号の到着時刻)は 波形データにおけるサンプル時刻と一致していなければならない。 また、第3列の値を文字列のbad (解析に用いるには適さない波形記録という意味) とすることができ、 この値を与えたデータは解析に用いられない。 The value of the 3rd column (the arrival time of the event signal) must be identical to a sample time in the waveform data. Also, a string bad is available for the value of the 3rd column, which means that the waveform record is not good for analysis; data with this value are skipped in the analysis. |
ファイル名を表す文字列。 A string that represents a file name. |
省略不可 Cannot be omitted |
| outputdir | 解析結果の出力先ディレクトリ名。 Name of the directory to output the results. |
ディレクトリ名を表す文字列。 A string that represents a directory name. |
省略不可 Cannot be omitted |
| Nrandom | 使用するランダムノイズ波形の個数(\(N_{random}\))。 The number of random noise traces to use (\(N_{random}\)). |
2以上の自然数。 A natural number (\(\geq 2\)). |
1000 |
| T_b_signal | パラメータ\(T_b^{signal}\)の値[s]。
イベント信号の到着時刻を\(t_{arriv}\)として
[\(t_{arriv}+T_b^{signal}\), \(t_{arriv}+T_e^{signal}\)]
のタイムウインドウ(シグナルウインドウ)が
自己相関関数の計算に用いられる。 The value of parameter \(T_b^{signal}\) [s]; the ACF is computed using data in a time window [\(t_{arriv}+T_b^{signal}\), \(t_{arriv}+T_e^{signal}\)] (a signal window), where \(t_{arriv}\) is the arrival time of the event signal. |
波形データのサンプル間隔の整数倍となる実数(\(\leq 0.0\))。 A real number (\(\leq 0.0\)), which is an integer multiple of the sampling interval of the waveform data. |
-0.5 |
| T_e_signal | パラメータ\(T_e^{signal}\)の値[s]。
イベント信号の到着時刻を\(t_{arriv}\)として
[\(t_{arriv}+T_b^{signal}\), \(t_{arriv}+T_e^{signal}\)]
のタイムウインドウ(シグナルウインドウ)が
自己相関関数の計算に用いられる。 The value of parameter \(T_e^{signal}\) [s]; the ACF is computed using data in a time window [\(t_{arriv}+T_b^{signal}\), \(t_{arriv}+T_e^{signal}\)] (a signal window), where \(t_{arriv}\) is the arrival time of the event signal. |
波形データのサンプル間隔の整数倍となる正の実数。 A positive real number, which is an integer multiple of the sampling interval of the waveform data. |
9.5 |
| T_b_noise | パラメータ\(T_b^{noise}\)の値[s]。
イベント信号の到着時刻を\(t_{arriv}\)として
[\(t_{arriv}\) \(+\) \(T_b^{noise}\),
\(t_{arriv}\) \(+\) \(T_e^{noise}\)]
のタイムウインドウ(ノイズウインドウ)が
波形のノイズレベルの評価に用いられる。 The value of parameter \(T_b^{noise}\) [s]; the noise level of each waveform is evaluated in a time window [\(t_{arriv}\) \(+\) \(T_b^{noise}\), \(t_{arriv}\) \(+\) \(T_e^{noise}\)] (a noise window), where \(t_{arriv}\) is the arrival time of the event signal. |
波形データのサンプル間隔の整数倍となる負の実数。 A negative real number, which is an integer multiple of the sampling interval of the waveform data. |
\(T_e^{noise}-\)\((T_e^{signal}\)\(-T_b^{signal})\) |
| T_e_noise | パラメータ\(T_e^{noise}\)の値[s]。
イベント信号の到着時刻を\(t_{arriv}\)として
[\(t_{arriv}+T_b^{noise}\), \(t_{arriv}+T_e^{noise}\)]
のタイムウインドウ(ノイズウインドウ)が
波形のノイズレベルの評価に用いられる。 The value of parameter \(T_e^{noise}\) [s]; the noise level of each waveform is evaluated in a time window [\(t_{arriv}+T_b^{noise}\), \(t_{arriv}+T_e^{noise}\)] (a noise window), where \(t_{arriv}\) is the arrival time of the event signal. |
波形データのサンプル間隔の整数倍となる負の実数(\(>T_b^{noise}\))。 A negative real number (\(>T_b^{noise}\)), which is an integer multiple of the sampling interval of the waveform data. |
\(T_b^{signal}\) |
| taper_st |
シグナルウインドウの先頭部に掛けるtaperの長さ
\(T_{taper}^{st}\)[s]。
[\(t_{arriv}+T_b^{signal}\),
\(t_{arriv}+T_b^{signal}+T_{taper}^{st}\)]
の範囲にcosineテーパーが用いられる。 Length of the taper at the beginning part of the signal window \(T_{taper}^{st}\) [s]; a cosine taper is applied to a time window [\(t_{arriv}+T_b^{signal}\), \(t_{arriv}+T_b^{signal}+T_{taper}^{st}\)]. |
波形データのサンプル間隔の整数倍となる非負の実数
(<\((T_e^{signal}-T_b^{signal})/2\))。 A non-negative real number (<\((T_e^{signal}-T_b^{signal})/2\)), which is an integer multiple of the sampling interval of the waveform data. |
\(|T_b^{signal}|\) |
| taper_en |
シグナルウインドウの末尾部に掛けるtaperの長さ
\(T_{taper}^{en}\)[s]。
[\(t_{arriv}+T_e^{signal}-T_{taper}^{en}\),
\(t_{arriv}+T_e^{signal}\)]
の範囲にcosineテーパーが用いられる。 Length of the taper at the end part of the signal window \(T_{taper}^{en}\) [s]; a cosine taper is applied to a time window [\(t_{arriv}+T_e^{signal}-T_{taper}^{en}\), \(t_{arriv}+T_e^{signal}\)]. |
波形データのサンプル間隔の整数倍となる非負の実数
(< \((T_e^{signal}-T_b^{signal})/2\))。 A non-negative real number (< \((T_e^{signal}-T_b^{signal})/2\)), which is an integer multiple of the sampling interval of the waveform data. |
\(T_{taper}^{st}\) |
| Nsamples_whitening | スペクトルの白色化に用いるサンプル数
(\(N_{samples}^{whitening}\))。
周波数領域において各サンプルの値を
そのサンプルを中心とする\(N_{samples}^{whitening}\)サンプルの
絶対値平均で割ることによって白色化する。 The number of samples used for a spectral whitening (\(N_{samples}^{whitening}\)); each sample in a frequency domain is divided by the absolute value average of \(N_{samples}^{whitening}\) samples centered on the frequency to whiten the spectrum. |
正の奇数。 A positive odd number. |
11 |
| hpc | 使用するバンドパスフィルターのハイパス(低周波)側のコーナー周波数[Hz]。 The corner frequency [Hz] at the high-pass (low-frequency) side of the band-pass filter to be applied. |
正の実数。 A positive real number. |
省略不可 Cannot be omitted |
| hpn | 使用するバンドパスフィルターのハイパス(低周波)側の極の数。
最小位相フィルターを時間の順方向と逆方向に1回ずつ掛けることによって
ゼロ位相フィルターを実現するが、
パラメータhpnでは最小位相フィルター1回あたりの極の数を指定する。 The number of poles at the high-pass (low-frequency) side of the band-pass filter to be applied. A zero-phase filter is realized by sequentially applying minimum phase filters in normal and reversed orders of time, and parameter hpn indicates the number of poles in each minimum phase filter. |
正の整数。 A positive integer. |
2 |
| lpc | 使用するバンドパスフィルターのローパス(高周波)側のコーナー周波数[Hz]。 The corner frequency [Hz] at the low-pass (high-frequency) side of the band-pass filter to be applied. |
パラメータhpcよりも大きな正の実数。 A positive real number greater than parameter hpc. |
省略不可 Cannot be omitted |
| lpn | 使用するバンドパスフィルターのローパス(高周波)側の極の数。
最小位相フィルターを時間の順方向と逆方向に1回ずつ掛けることによって
ゼロ位相フィルターを実現するが、
パラメータlpnでは最小位相フィルター1回あたりの極の数を指定する。 The number of poles at the low-pass (high-frequency) side of the band-pass filter to be applied. A zero-phase filter is realized by sequentially applying minimum phase filters in normal and reversed orders of time, and parameter lpn indicates the number of poles in each minimum phase filter. |
正の整数。 A positive integer. |
2 |
| SNratio_min | 解析に使用するシグナル/ノイズ比の下限。
シグナルウインドウでの標準偏差とノイズウインドウでの標準偏差の比が
この値を下回る波形は解析に使用しない。 The lower limit of a signal-to-noise ratio to use a waveform for the analysis. A waveform is not used for the analysis if the ratio of standard deviations in the signal window to the noise window is less than this value. |
非負の実数。0.0を指定すれば下限無しとなる。 A non-negative real number; 0.0 results in no lower limit. |
1.0 |
| output_filtered_impulse | \(\delta\)関数のフィルター応答波形(filtered_impulse.seq2)
の出力の有無。 Whether to output the filter response waveform of \(\delta\) function (filtered_impulse.seq2). |
|
yes |
| output_individual_event_results | 個々のイベント毎の反射応答の出力の有無。 Whether to output the reflection responses from individual events. |
|
yes |
| verbose | 進行状況の表示の有無。 Whether to display the progress. |
|
yes |
|
#event1 (no data for station3) event1[TAB]station1.sac[TAB]12.3 event1[TAB]station2.sac[TAB]12.4 event1[TAB]station4.sac[TAB]13.5 #event2 event2[TAB]station1.sac[TAB]14.1 event2[TAB]station1.sac[TAB]bad event2[TAB]station3.sac[TAB]14.0 event2[TAB]station5.sac[TAB]13.8 #event3 event3[TAB]station2.sac[TAB]20.1 event3[TAB]station3.sac[TAB]20.2 event3[TAB]station4.sac[TAB]20.0 event3[TAB]station5.sac[TAB]20.3 #event4 event4[TAB]station3.sac[TAB]15.0 event4[TAB]station4.sac[TAB]14.5 |