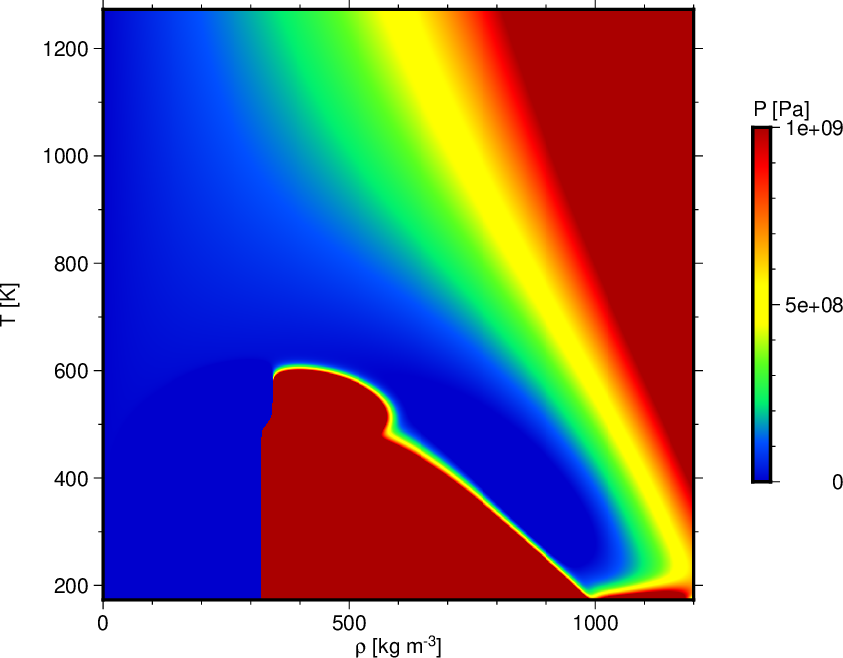
図1. 密度\(\rho\)と温度\(T\)の関数としての圧力\(P\)。
Fig. 1. The pressure \(P\) as a function of the density \(\rho\) and temperature \(T\).
 図1. 密度\(\rho\)と温度\(T\)の関数としての圧力\(P\)。 Fig. 1. The pressure \(P\) as a function of the density \(\rho\) and temperature \(T\). |
図2. 温度\(T=700\) [K]における密度\(\rho\)の関数としての圧力\(P\)。 Fig. 2. The pressure \(P\) as a function of the density \(\rho\) at a temperature \(T=700\) [K]. |
図3. 温度\(T=600\) [K]における密度\(\rho\)の関数としての圧力\(P\)。 Fig. 3. The pressure \(P\) as a function of the density \(\rho\) at a temperature \(T=600\) [K]. |
図4. 温度\(T=300\) [K]における密度\(\rho\)の関数としての圧力\(P\)。 Fig. 4. The pressure \(P\) as a function of the density \(\rho\) at a temperature \(T=300\) [K]. |
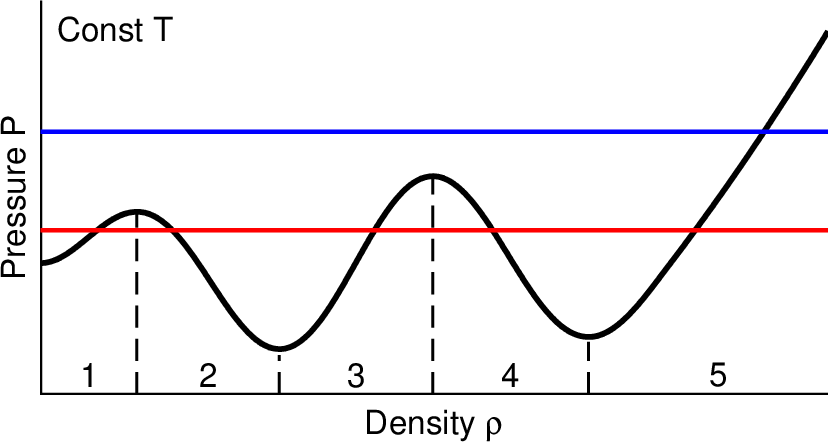 図5. 一定温度での密度と圧力の関係の模式図。 Fig. 5. A schematic view of the relation between the density and pressure at a constant temperature. |
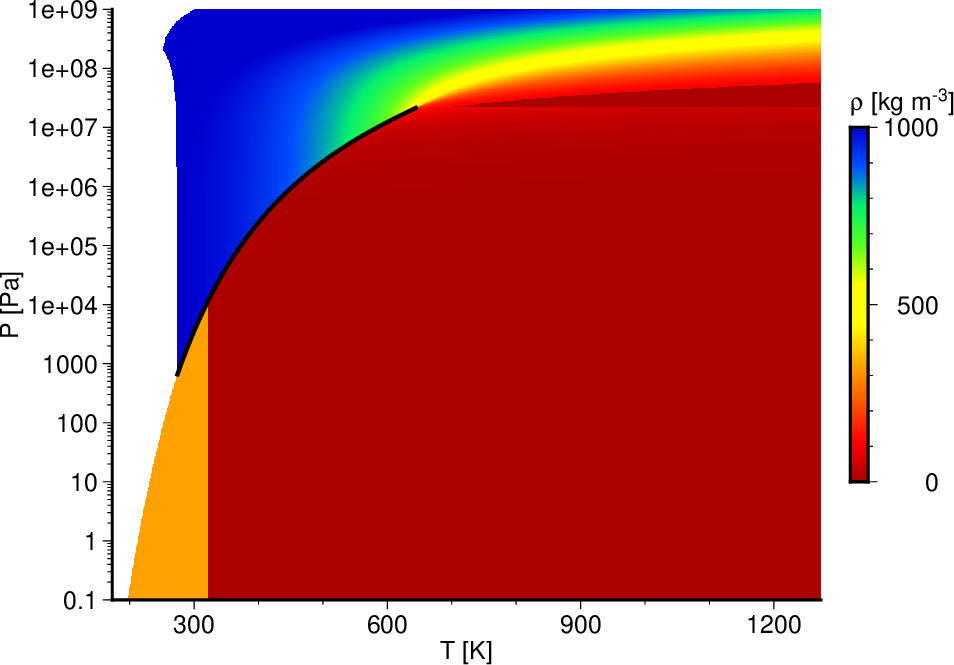 図6. 古い関数IAPWS95_calculate_min_density_givenTP (気相), IAPWS95_calculate_max_density_givenTP (液相・超臨界流体) を用いて計算した各温度\(T\), 圧力\(P\)での密度\(\rho\)。 黒線は気液相境界。 低温の気体や低圧の超臨界流体において密度が正しく求まっていない。 Fig. 6. The densities \(\rho\) for each temperature \(T\) and pressure \(P\) calculated with old functions IAPWS95_calculate_min_density_givenTP (for the gas phase) and IAPWS95_calculate_max_density_givenTP (for the liquid phase and supercritical fluid). The black line is the liquid-gas boundary. The densities are not correct for low-temperature gas and low-pressure supercritical fluid. |
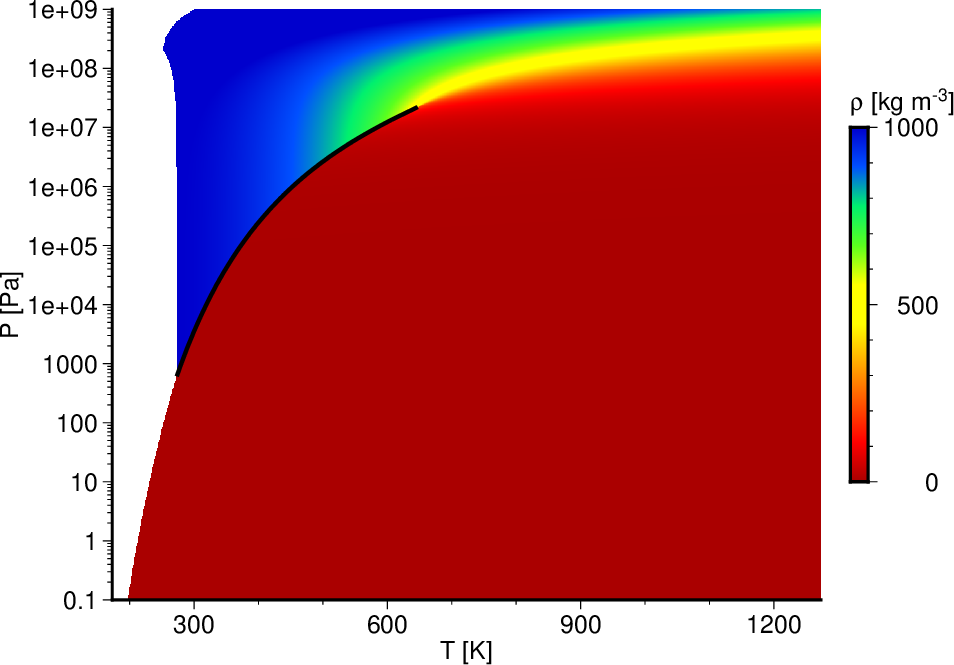 図7. 改良した関数IAPWS95_calculate_density_givenTP_liquid (液相), IAPWS95_calculate_density_givenTP_gas (気相), IAPWS95_calculate_density_givenTP_supercritical (超臨界流体) を用いて計算した各温度\(T\), 圧力\(P\)での密度\(\rho\)。 黒線は気液相境界。 Fig. 7. The densities \(\rho\) for each temperature \(T\) and pressure \(P\) calculated with improved functions IAPWS95_calculate_density_givenTP_liquid (for the liquid phase), IAPWS95_calculate_density_givenTP_gas (for the gas phase), and IAPWS95_calculate_density_givenTP_supercritical (for the supercritical fluid). The black line is the liquid-gas boundary. |
| 関数名 Function name |
機能・用途 Purpose |
| IAPWS95_calculate_min_density_givenTP 【使用非推奨】 [Discouraged to use] | Wagner and Pruss (2002)の状態方程式を用いて
指定された温度・圧力を与える最小の密度を計算する。 Compute the minimum density which satisfies the given temperature and pressure using the equation of state of Wagner and Pruss (2002). |
| IAPWS95_calculate_max_density_givenTP 【使用非推奨】 [Discouraged to use] | Wagner and Pruss (2002)の状態方程式を用いて
指定された温度・圧力を与える最大の密度を計算する。 Compute the maximum density which satisfies the given temperature and pressure using the equation of state of Wagner and Pruss (2002). |
| IAPWS95_calculate_density_givenTP_liquid | Wagner and Pruss (2002)の状態方程式を用いて
指定された温度・圧力を与える密度(液相)を計算する。 Compute the density of the liquid phase for given temperature and pressure using the equation of state of Wagner and Pruss (2002). |
| IAPWS95_calculate_density_givenTP_gas | Wagner and Pruss (2002)の状態方程式を用いて
指定された温度・圧力を与える密度(気相)を計算する。 Compute the density of the gas phase for given temperature and pressure using the equation of state of Wagner and Pruss (2002). |
| IAPWS95_calculate_density_givenTP_supercritical | Wagner and Pruss (2002)の状態方程式を用いて
指定された温度・圧力を与える密度(超臨界流体)を計算する。 Compute the density of the supercritical fluid for given temperature and pressure using the equation of state of Wagner and Pruss (2002). |
| IAPWS95_calculate_density_givenTP | Wagner and Pruss (2002)の状態方程式を用いて
指定された温度・圧力を与える密度を計算する。
相は温度・圧力に基づいて自動で判定する。 Compute the density for given temperature and pressure using the equation of state of Wagner and Pruss (2002). The phase is automatically identified from the given temperature and pressure. |