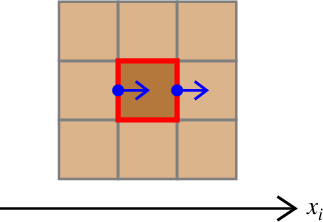
図1. 赤色の格子セルの中心点にシングルフォース成分\(F_i\)を作用させるための 等価体積力(青)の組合せ。
Fig. 1. Combination of equivalent body forces (blue) to achieve a single force component \(F_i\) at the center of the red grid cell.
 図1. 赤色の格子セルの中心点にシングルフォース成分\(F_i\)を作用させるための 等価体積力(青)の組合せ。 Fig. 1. Combination of equivalent body forces (blue) to achieve a single force component \(F_i\) at the center of the red grid cell. |
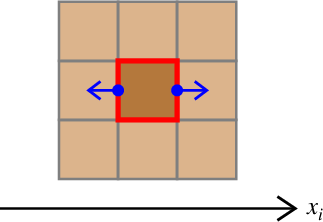 図2. 赤色の格子セルの中心点にモーメントテンソルの対角成分\(M_{ii}\)を作用させるための 等価体積力(青)の組合せ。 Fig. 2. Combination of equivalent body forces (blue) to achieve a diagonal moment tensor component \(M_{ii}\) at the center of the red grid cell. |
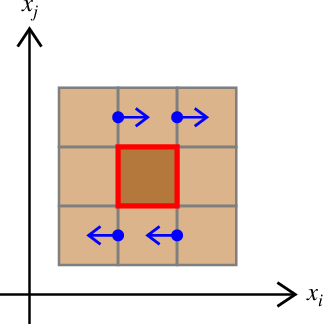 図3. 赤色の格子セルの中心点にモーメントテンソルの非対角成分\(M_{ij}\)を作用させるための 等価体積力(青)の組合せ。 Fig. 3. Combination of equivalent body forces (blue) to achieve a off-diagonal moment tensor component \(M_{ij}\) at the center of the red grid cell. |