winvコマンドマニュアル

(The documentation of winv command)

Last Update: 2024/8/6

◆機能・用途(Purpose)

Maeda et al. (2011)のアルゴリズムにより火山性地震の力源に関する波形逆解析を行う。
Perform waveform inversion for the source mechanism of a volcano-seismic event using an algorithm proposed by Maeda et al. (2011).

◆ソースコード(Source code)

$YMAEDA_OPENTOOL_DIR/winv/src/winv.c

◆使用方法(Usage)

コマンドライン引数でパラメータを指定する。パラメータの一覧を下表に示す。
Specify parameters by command-line arguments. The table below shows a list of parameters.

●「-」から始まらない引数 (Arguments not beginning with “-”)

このコマンドでは「-」から始まらない引数は存在しない。
This command does not have arguments not beginning with “-”.

●1つの「-」から始まる引数 (Arguments beginning with a single “-”)

このコマンドでは1つの「-」から始まる引数は存在しない。
This command does not have arguments beginning with a single “-”.

●「--パラメータ名=パラメータ値」の形式の引数 (Arguments of a form “--Parameter name=Parameter Value”)

「--パラメータ名=パラメータ値」の形式の引数は自由な順番で指定できる。「-」から始まらない引数の間に挿入しても良い。相反する指定がなされた場合には後の指定が優先される。
Arguments of a form “--Parameter name=Parameter Value” can be placed in an arbitrary order. They can even be inserted between arguments not beginning with “-”. In case of conflicting options being specified, the latter option has a higher priority.

(1)仮定する力源に関するパラメータ (Parameters for assumed source mechanism)
一般に地震の力源はシングルフォース3成分の時空間分布 $F_x(x,y,z,t)$, $F_y(x,y,z,t)$, $F_z(x,y,z,t)$ およびモーメントテンソル6成分の時空間分布 $M_{xx}(x,y,z,t)$, $M_{yy}(x,y,z,t)$, $M_{zz}(x,y,z,t)$, $M_{xy}(x,y,z,t)$, $M_{yz}(x,y,z,t)$, $M_{zx}(x,y,z,t)$ によって表現できる。なお \[\begin{equation} M_{yx}(x,y,z,t)=M_{xy}(x,y,z,t) \label{eq.Myx} \end{equation}\] \[\begin{equation} M_{zy}(x,y,z,t)=M_{yz}(x,y,z,t) \label{eq.Mzy} \end{equation}\] \[\begin{equation} M_{xz}(x,y,z,t)=M_{zx}(z,y,z,t) \label{eq.Mxz} \end{equation}\] であるものとする。このプログラムでは 位置を直交座標系で表す。 $x$が東方向、$y$が北方向、$z$が上方向 とする。 $t$は時刻を表す。
In general, the source of a seismic event is expressed by spatiotemporal distributions of three single force components $F_x(x,y,z,t)$, $F_y(x,y,z,t)$, $F_z(x,y,z,t)$ and six moment tensor components $M_{xx}(x,y,z,t)$, $M_{yy}(x,y,z,t)$, $M_{zz}(x,y,z,t)$, $M_{xy}(x,y,z,t)$, $M_{yz}(x,y,z,t)$, $M_{zx}(x,y,z,t)$, assuming that Eqs. (\ref{eq.Myx})-(\ref{eq.Mxz}) hold. This program expresses a location by cartesian coordinate system, in which $x$-, $y$-, and $z$-axes are taken eastward, northward, and upward, respectively; $t$ represents time.

このプログラムではシングルフォースとモーメントテンソルの時空間分布を $M$個の要素ソースの組合せで \[\begin{equation} \begin{pmatrix} F_x(x,y,z,t) \\ F_y(x,y,z,t) \\ F_z(x,y,z,t) \end{pmatrix} =\sum_{m=0}^{M-1} \begin{pmatrix} F_x^{(m)} \\ F_y^{(m)} \\ F_z^{(m)} \end{pmatrix} f_m(x,y,z) s_m(t) \label{eq.source.F} \end{equation}\] \[\begin{eqnarray} & & \begin{pmatrix} M_{xx}(x,y,z,t) & M_{xy}(x,y,z,t) & M_{xz}(x,y,z,t) \\ M_{yx}(x,y,z,t) & M_{yy}(x,y,z,t) & M_{yz}(x,y,z,t) \\ M_{zx}(x,y,z,t) & M_{zy}(x,y,z,t) & M_{zz}(x,y,z,t) \end{pmatrix} \nonumber \\ &=& \sum_{m=0}^{M-1} \begin{pmatrix} M_{xx}^{(m)} & M_{xy}^{(m)} & M_{xz}^{(m)} \\ M_{yx}^{(m)} & M_{yy}^{(m)} & M_{yz}^{(m)} \\ M_{zx}^{(m)} & M_{zy}^{(m)} & M_{zz}^{(m)} \end{pmatrix} f_m(x,y,z) s_m(t) \label{eq.source.M} \end{eqnarray}\] と表現する。この $s_m(t)$ ($m=0,1,\cdots,M-1$)が逆解析で求める未知パラメータ である。$s_m(t)$は 震源時間関数 と呼ばれる。
This program expresses the spatiotemporal distributions of single force and moment tensor components by a combination of $M$ elementary sources as Eqs. (\ref{eq.source.F}) and (\ref{eq.source.M}). These $s_m(t)$ ($m=0,1,\cdots,M-1$) are unknown parameters to be solved by inversion and referred to as source time functions.

$f_m(x,y,z)$はユーザが与える(仮定する)関数 であり、力源の強度の空間分布を表す。ある基準点$(x_m^{ref},y_m^{ref},z_m^{ref})$からの距離の関数として与える。基準点としては力源の強度の重心である セントロイド $(x_c,y_c,z_c)$ を用いるのが分かりやすい。火山性地震の力源の逆解析においては点ソースを仮定する場合がほとんどであり、このときは \[\begin{equation} f_m(x,y,z)=\delta(x-x_c)\delta(y-y_c)\delta(z-z_c) \label{eq.fm.point_source} \end{equation}\] とする。ここで$\delta()$はディラックのデルタ関数を表す。セントロイドからずれた位置に点ソースを与えることもできる。例えば$z$方向に距離$h$だけ離れた2つの点ソース $(x_c,y_c,z_c-h/2)$, $(x_c,y_c,z_c+h/2)$ の組で力源を表現する問題設定も可能であり、この場合は \[\begin{equation} f_1(x,y,z)=\delta(x-x_c)\delta(y-y_c)\delta(z-z_c+h/2) \label{eq.f1.point_source.zc_h} \end{equation}\] \[\begin{equation} f_2(x,y,z)=\delta(x-x_c)\delta(y-y_c)\delta(z-z_c-h/2) \label{eq.f2.point_source.zc_h} \end{equation}\] とする。
The function $f_m(x,y,z)$ is supposed to be given (assumed) by the user and represents the spatial distribution of the source intensity. It is given as a function of the distance from a reference point $(x_m^{ref},y_m^{ref},z_m^{ref})$. For the reference point, the weight center of the source intensity $(x_c,y_c,z_c)$, known as the centroid, is recommended to be used. Most waveform inversion for the source mechanism of volcano-seismic events assumes a point source given by Eq. (\ref{eq.fm.point_source}), where $\delta()$ denotes Dirac's delta function. A point source can be given at a location different from the centroid. For example, consider to assume two point sources at distance $h$ along the $z$-direction. This problem is realized by Eqs. (\ref{eq.f1.point_source.zc_h}) and (\ref{eq.f2.point_source.zc_h}); these equations define two point sources at $(x_c,y_c,z_c-h/2)$ and $(x_c,y_c,z_c+h/2)$.

(\ref{eq.source.F})(\ref{eq.source.M})式の $F_p^{(m)}$, $M_{pq}^{(m)}$ ($p,q=x,y,z$)はユーザが与える(仮定する)定数 である。これらは$m$番目の要素ソースのメカニズムを表しており、その与え方によって問題設定が変わってくる。例えば$M=9$, $F_x^{(0)}=1$, $F_y^{(1)}=1$, $F_z^{(2)}=1$, $M_{xx}^{(3)}=1$, $M_{yy}^{(4)}=1$, $M_{zz}^{(5)}=1$, $M_{xy}^{(6)}=M_{yx}^{(6)}=1$, $M_{yz}^{(7)}=M_{zy}^{(7)}=1$, $M_{zx}^{(8)}=M_{xz}^{(8)}=1$ とし、他の全ての$F_p^{(m)}$, $M_{pq}^{(m)}$成分を0とすればシングルフォース3成分とモーメントテンソル6成分の時間関数を独立に直接求める逆解析 (Ohminato et al. 1998)になる。また$M=1$として \[\begin{equation} \begin{pmatrix} F_x^{(m)} \\ F_y^{(m)} \\ F_z^{(m)} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \label{eq.Nakano.F} \end{equation}\] \[\begin{eqnarray} & & \begin{pmatrix} M_{xx}^{(m)} & M_{xy}^{(m)} & M_{xz}^{(m)} \\ M_{yx}^{(m)} & M_{yy}^{(m)} & M_{yz}^{(m)} \\ M_{zx}^{(m)} & M_{zy}^{(m)} & M_{zz}^{(m)} \end{pmatrix} \nonumber \\ &=& \begin{pmatrix} 2\sin^2\theta\cos^2\phi+1 & 2\sin^2\theta\sin\phi\cos\phi & 2\sin\theta\cos\theta\cos\phi \\ 2\sin^2\theta\sin\phi\cos\phi & 2\sin^2\theta\sin^2\phi+1 & 2\sin\theta\cos\theta\sin\phi \\ 2\sin\theta\cos\theta\cos\phi & 2\sin\theta\cos\theta\sin\phi & 2\cos^2\theta+1 \end{pmatrix} \label{eq.Nakano.M} \end{eqnarray}\] とすれば開口クラックを仮定した逆解析(Nakano and Kumagai 2005)になる。ここで$\theta$, $\phi$はクラックの法線ベクトルの方向を表し、これらを固定値として与えることもできるし、グリッドサーチで最適値を求めることもできる。同様の考え方で$M=2$として2枚の開口クラックを仮定した逆解析 (Chouet et al. 2005)を行うこともできる。
On the contrary, $F_p^{(m)}$, $M_{pq}^{(m)}$ ($p,q=x,y,z$) are constants given (assumed) by the user. They represent the mechanism of $m$th elementary source, and the definitions of them determines the problem. For example, inversion for directly solving the time functions of the three single force and six moment tensor components independently (Ohminato et al. 1998) is realized by using $M=9$, $F_x^{(0)}=1$, $F_y^{(1)}=1$, $F_z^{(2)}=1$, $M_{xx}^{(3)}=1$, $M_{yy}^{(4)}=1$, $M_{zz}^{(5)}=1$, $M_{xy}^{(6)}=M_{yx}^{(6)}=1$, $M_{yz}^{(7)}=M_{zy}^{(7)}=1$, $M_{zx}^{(8)}=M_{xz}^{(8)}=1$, and zero for all other $F_p^{(m)}$ and $M_{pq}^{(m)}$ components. Inversion assuming a tensile crack source (Nakano and Kumagai 2005) is realized by setting $M=1$ and Eqs. (\ref{eq.Nakano.F}) and (\ref{eq.Nakano.M}), where $\theta$ and $\phi$ defines the crack normal direction; they can either be fixed, or investigated by grid searches. Inversion for two intersecting tensile cracks (Chouet et al. 2005) is realized in a similar way with $M=2$.

上の例の$\theta$, $\phi$のように $F_p^{(m)}$, $M_{pq}^{(m)}$をパラメータを含む数式で与えてそれらのパラメータをグリッドサーチで求める場合、これらのパラメータを本マニュアルでは 発震機構パラメータ と呼ぶ。
In case of expressing $F_p^{(m)}$, $M_{pq}^{(m)}$ using equations that consist of parameters and determine the optimal parameter values, as $\theta$ and $\phi$ in the example above, these parameters are called focal mechanism parameters in this documentation.

仮定する$F_p^{(m)}$, $M_{pq}^{(m)}$, および$f_m(x,y,z)$に関するパラメータを下表に示す。
The table below shows the parameters for the assumed $F_p^{(m)}$, $M_{pq}^{(m)}$, and $f_m(x,y,z)$.

パラメータ名 Parameter name	意味 Meaning	可能なパラメータ値 Allowed parameter values	デフォルト値 Default value
modelseq_list_file	使用する要素ソースの設定ファイル名。 The name of a configuration file that determines the elementary sources to use.	ファイル名を表す文字列。 A string that represents a file name. ファイルの書式 (File format)	modelseq.list
M	使用する要素ソースの個数 ((\ref{eq.source.F})(\ref{eq.source.M})式の$M$の値)。 The number of elementary sources; the value of $M$ in Eqs. (\ref{eq.source.F}) and (\ref{eq.source.M}).	パラメータmodelseq_list_fileで指定するファイルの空行・コメントを除いた行数($M_{max}$)以下の正の整数。なお$M<M_{max}$の場合にはパラメータmodelseq_list_fileで指定するファイルでの登場順に最初の$M$個の要素ソースが用いられる。 A positive integer less than or equal to the number of lines $M_{max}$ (excluding empty lines and comments) of the file specified by parameter modelseq_list_file. If $M<M_{max}$, only the first $M$ elementary sources (based on the order in the file specified by parameter modelseq_list_file) are used.	$M_{max}$

(2)入力データに関するパラメータ (Parameters for input data)
winvコマンドでは 各観測・各成分のイベント波形が入力データ である。一般に、利用できる波形の成分は観測点によってまちまちである。例えばある観測点では上下、南北、東西の3成分の波形を利用できるが別の観測点では上下動しか利用できないというケースがある。それゆえ観測点を単位として取り扱うと処理が煩雑になる。そこでwinvコマンドでは観測データを観測点や成分ではなくその組合せ(トレース)を単位として扱う。例えば2つの観測点STN1, STN2を利用し、 STN1ではEW, NS, UDの3成分があるがSTN2ではUD成分のみが利用可能な場合、 STN1.EW, STN1.NS, STN1.UD, STN2.UDの4トレースとなる。これらを全く独立な4本の波形として (STN1.EW, STN1.NS, STN1.UDが同じ地点での波形であることや STN1.UD, STN2.UDが同じ方向成分の波形であることは一切考慮せずに) 取り扱う。
The input data for winv command is the waveforms for each component at each station. In general, available waveform components depend on stations. For example, the vertical, NS, and EW components may be available at some stations, whereas only the vertical component may be available at some other stations. Therefore, treatments based on station unit would be complicated. To simplify the treatment, the winv command uses a concept of a trace, which is a combination of a station and a component. For example, suppose that two stations STN1 and STN2 are available; three components (EW, NS, and UD) are available at the station STN1, whereas only the UD component is available at STN2. In this case, the traces are STN1.EW, STN1.NS, STN1.UD, and STN2.UD. The waveforms for these four traces are treated independently, without using information that the traces STN1.EW, STN1.NS, and STN1.UD are at the same location and the traces STN1.UD and STN2.UD are the same directional component.

観測波形に見られるシグナルが (\ref{eq.source.F})(\ref{eq.source.M})式の力源によって生じたと仮定すると、 $n$番目のトレースの観測波形と力源の間には \[\begin{equation} u_n(t)=\sum_{m=0}^{M-1} s_m(t)∗\left[ g_{nm}^{trans}(t)∗i_n^{trans}(t) +g_{nm}^{tilt}(t)∗i_n^{tilt}(t) \right] \label{eq.u_n} \end{equation}\] の関係が成り立つ(Maeda et al. 2011)。ここで$∗$はコンボリューションを表す。 $g_{nm}^{trans}(t)$, $g_{nm}^{tilt}(t)$は $m$番目の要素ソース)において$s_m(t)=\delta(t)$とした場合に $n$番目のトレースに生じると理論的に期待される変位波形および傾斜変動波形であり、 $m$番目の要素ソースに対する グリーン関数 と見なせる。 $i_n^{trans}(t)$, $i_n^{tilt}(t)$は $n$番目のトレースにおける地震計の並進応答および傾斜応答を表す。地震計は実際の地面の動きをそのまま記録するわけではない。 $n$番目のトレースにおいて実際の地面の変位が$\delta(t)$で傾斜変動が0の場合に地震計で記録されると理論的に期待されるシグナルが$i_n^{trans}(t)$であり、実際の地面の変位が0で傾斜変動が$\delta(t)$の場合に地震計で記録されると理論的に期待されるシグナルが$i_n^{tilt}(t)$である。 winvコマンドでは観測波形$u_n(t)$を用いて (\ref{eq.u_n})式と等価な関係式に基づき震源時間関数$s_m(t)$の推定が行われる。
The observed waveform of $n$th trace is related to the source forces through Eq. (\ref{eq.u_n}) if the signal in the waveform was caused by the source mechanism given by Eqs. (\ref{eq.source.F}) and (\ref{eq.source.M}), where $∗$ represents a convolution (Maeda et al. 2011). Here, $g_{nm}^{trans}(t)$ and $g_{nm}^{tilt}(t)$ are theoretical displacement and tilt of $n$th trace, respectively, caused by $m$th elementary source with $s_m(t)=\delta(t)$; they can be regarded as Green’s function for $m$th elementary source. Functions $i_n^{trans}(t)$ and $i_n^{tilt}(t)$ denote translational and tilt responses of the seismometer for $n$th trace, respectively. The seismometer does not perfectly record the ground motion; $i_n^{trans}(t)$ is a theoretical signal of the seismometer if the actual ground displacement is $\delta(t)$ and the actual ground tilt is zero, and $i_n^{tilt}(t)$ is a theoretical signal of the seismometer if the actual ground displacement is zero and the actual ground tilt is $\delta(t)$. The winv command estimates the source time functions $s_m(t)$ from the observed waveforms $u_n(t)$ using a relation equivalent to Eq. (\ref{eq.u_n}).

イベント波形は以下の要領で用意する。
A guideline for the preparation of event waveforms is given below.

速度波形(m/s)または変位波形(m)を用意する。速度波形を用いる場合には(\ref{eq.u_n})式を時間で微分した関係式 \[\begin{equation} \frac{du_n(t)}{dt}=\sum_{m=0}^{M-1} s_m(t)∗\left[ \frac{dg_{nm}^{trans}(t)}{dt}∗i_n^{trans}(t) +\frac{dg_{nm}^{tilt}(t)}{dt}∗i_n^{tilt}(t) \right] \label{eq.u_n.time_derivative} \end{equation}\] と等価な式が逆解析で用いられる。
Prepare velocity (m/s) or displacement (m) waveforms. If the velocity waveforms are used, the inversion uses a relation equivalent to Eq. (\ref{eq.u_n.time_derivative}), which is a temporal derivative of Eq. (\ref{eq.u_n}).
生波形でもフィルターを掛けた波形でも良い。フィルターを掛けた波形を用いた場合には得られる震源時間関数$s_m(t)$にも同じフィルターが掛かることになる。
The waveforms can be raw or filtered; if filtered waveforms are used, the source time function $s_m(t)$ to be derived is band-limited with the same filter.
地震計の応答特性は(\ref{eq.u_n})式の右辺において考慮されている。入力データとしてプログラムに渡すべき量は (\ref{eq.u_n})式の左辺の$u_n(t)$であるので 入力データから応答特性は除去しない ことを基本とする。
Instrumental responses of seismometers should not be removed from the input waveforms, as the data should be $u_n(t)$ in the left hand side of Eq. (\ref{eq.u_n}) whereas the responses are accounted for in the right hand side of this equation.
波形はSeismic Analysis Code (SAC)の時系列データとして 1つのディレクトリ内にまとめて入れる。
Prepare the waveforms as time series data in Seismic Analysis Code (SAC) format, and store them in a single directory.
データは絶対日時の情報を含んでいなければならない。
The data must have information on absolute date and time.

入力データに関するパラメータを下表に示す。
The table below shows the parameters for the input data.

パラメータ名 Parameter name	意味 Meaning	可能なパラメータ値 Allowed parameter values	デフォルト値 Default value
datadir	使用する波形データ(SAC形式の時系列データ)が格納されているディレクトリパス。 A directory path in which the waveform data (time series data in SAC format) are stored.	ディレクトリパスを表す文字列。 A string that represents a directory path.	data
cut_st	解析に使用する時間窓の先頭。 The beginning of the time window used for the analysis.	日付・時刻を表す文字列。年、月、日、時、分、秒をカンマ(,)で区切って並べる。秒は実数で与え、ほかは整数で与える。頭に0は付けない。 A string that represents a date and time, expressed as the year, month, day, hour, minute and second separated by commas (,). Use a real number for the second, and integers for the other values. Do not append 0 at the top of each value.	省略不可 Cannot be omitted
cut_en	解析に使用する時間窓の末尾。 The end of the time window used for the analysis.	cut_stよりも後の日付・時刻を表す文字列。年、月、日、時、分、秒をカンマ(,)で区切って並べる。秒は実数で与え、ほかは整数で与える。頭に0は付けない。 A string that represents a date and time later than cut_st, expressed as the year, month, day, hour, minute and second separated by commas (,). Use a real number for the second, and integers for the other values. Do not append 0 at the top of each value.	省略不可 Cannot be omitted
taper_st	使用する波形の後半に掛けるテーパーの開始時刻。 The beginning time of a taper applied to a later part of waveforms used.	cut_stよりも後、cut_enよりも前の日付・時刻を表す文字列。年、月、日、時、分、秒をカンマ(,)で区切って並べる。秒は実数で与え、ほかは整数で与える。頭に0は付けない。 A string that represents a date and time later than cut_st and earlier than cut_en, expressed as the year, month, day, hour, minute and second separated by commas (,). Use a real number for the second, and integers for the other values. Do not append 0 at the top of each value.	省略不可 Cannot be omitted

(3)グリーン関数に関するパラメータ (Parameters for Green’s functions)
winvコマンドではグリーン関数を waterPMLコマンドを用いて計算することを想定している。 waterPMLコマンドで計算する量はインパルス$\delta(t)$に対する応答(グリーン関数)ではなく、有限の時定数を持つ震源時間関数$s^{green}(t)$によって生じる理論波形であり、 \[\begin{equation} \tilde{g}_{nm}^{trans}(t)\equiv s^{green}(t)∗g_{nm}^{trans}(t), \hspace{1em} \tilde{g}_{nm}^{tilt}(t)\equiv s^{green}(t)∗g_{nm}^{tilt}(t) \label{eq.practical_Green} \end{equation}\] と書ける。以下ではこれらを 実用グリーン関数と呼ぶ。
The winv command assumes that Green’s functions have been computed using waterPML command. However, it does not compute the response to an impulse $\delta(t)$ (Green’s functions) but theoretical waveforms (Eq. \ref{eq.practical_Green}) generated by a source time function $s^{green}(t)$ with a finite time constant. These are referred to as practical Green’s functions in the following.

winvコマンドによる波形逆解析ではソース位置を仮定する必要がある。なお、火山性地震の波形逆解析の多くは点ソース(\ref{eq.fm.point_source}式)を仮定するのでここでは点ソースを念頭に置いて説明するが、有限サイズのソースの場合にはそれを1点で代表させた位置 (震源やセントロイドなど)と読み替えれば良い。火山の長周期・超長周期地震等のイベントにおいてはソース位置も未知である場合が多い。そこで、ソース位置を仮定した波形逆解析を全てのソース候補位置について繰り返し行い、観測波形と合成波形の残差が最小になる位置を探索(グリッドサーチ)する必要がある。そのためには全てのソース候補位置とトレースのペアについて実用グリーン関数が必要になる。
A source location must be assumed in the waveform inversion of winv command; here, a point source (Eq. \ref{eq.fm.point_source}) is assumed because most waveform inversion of volcano-seismic signals assumes a point source. In case of an extended source, regard the “source location” as a representative location of the source (e.g., a hypocenter or a centroid). The source location is often unknown, especially in case of volcanic long-period and very-long-period events. Therefore, inversion with an assumed source location must be repeated for all candidate source locations, and the optimal location that minimizes the residual between observed and synthetic waveforms must be searched (a grid search). In this approach, practical Green’s functions are needed for the pairs of all candidate source locations and all traces.

waterPMLコマンドを用いた波動場の計算では 1度の計算で1つのソース位置・成分と全ての観測点位置・成分のペアについて実用グリーン関数が得られる。ソース候補位置が多い場合、ソースと観測点を入れ替えても結果は変わらないという性質(相反定理)に基づき観測点側にソースを置いて実用グリーン関数を計算することで計算回数を減らすことができる。
Each run of waterPML command computes practical Green’s functions from one source location and component to all station locations and components. In case of abundant candidate source locations, the number of computations can be reduced by placing the seismic wave source at a station side; an waveform does not change by swapping a source and a station (a reciprocity theorem).

このような考え方に基づき、 winvコマンドで使用する実用グリーン関数は waterPMLコマンドを用いて以下のように行う。 各観測点の位置(図1の水色のセル)において、使用する観測データの各成分と同じ方向のシングルフォース(図1の黒矢印→) を地震波動ソースとして与え、波動場を計算する。相反定理を用いることをプログラムに知らせるため、ソースメカニズムとして(Fx, Fy, Fzではなく)Vx, Vy, Vzを使用する。実用グリーン関数は位置の関数であるスナップショットとして出力する。その際に--snapshot_place=dオプションを付ける。ソース位置の候補範囲(図1の赤枠)を囲む格子セル (図1の★) の1つ外のセルまで(図1の黒枠の範囲)を出力範囲とする。
Therefore, compute the practical Green’s functions for winv command using waterPML command as follows. Compute a wave field using a single force source at a station location (the blue cell in Fig. 1); the direction of the force must be equal to that of one of the observation components of this station (the black arrow → in Fig. 1). To inform the use of the reciprocity theorem to the program, use Vx, Vy, or Vz (instead of Fx, Fy, or Fz) as the source mechanism. Output the practical Green’s functions as snapshots, i.e., functions of locations. Use --snapshot_place=d option. The output region of the snapshot is determined as follows. Let the red rectangle in Fig. 1 be the spatial extent of candidate source locations. Grid cells that bound this region are shown by ★. The output range of the snapshots is up to one grid cell outside of these cells (the black rectangle in Fig. 1).

スナップショットには速度3成分が含まれる。相反定理によれば、例えばシングルフォース$F_x$を観測点位置に与えたときのソース位置での速度$V_y$はソース位置にシングルフォース$F_y$を与えたときの観測点位置での速度$V_x$に等しい。したがって、スナップショットには全てのソース候補位置におけるシングルフォース3成分と1つのトレースのペアに対する速度の実用グリーン関数が含まれることになる。また、--snapshot_place=dオプションを用いることで格子セルの境界面にシングルフォースソースを置いた実用グリーン関数(速度)が得られ (図1の青矢印→↑)、これらを組み合わせることで格子セルの中心点におけるモーメントテンソル6成分に対する速度の実用グリーン関数を合成することができる。これらの線形結合により、格子セル中心点における要素ソースに対する速度の実用グリーン関数$d\tilde{g}_{nm}^{trans}(t)/dt$ が得られる。
The snapshots consist of the three velocity components. The reciprocity theorem tells that, for example, a velocity component $V_y$ at a source location caused by a single force component $F_x$ at a station location is equal to a velocity component $V_x$ at the station location caused by a single force component $F_y$ at the source location. Therefore, the snapshots include practical velocity Green’s functions from the three single forces at all candidate source locations to a trace. The --snapshot_place=d option in the waterPML command results in practical Green’s functions (velocities) from single forces on the interfaces of grid cells (the blue arrows →↑ in Fig. 1). They can be combined to synthesize practical velocity Green’s functions from six moment tensor components at the center of each grid cell. Linear combinations of them give practical velocity Green’s functions $d\tilde{g}_{nm}^{trans}(t)/dt$ for elementary sources from the center of each grid cell.

図1. 実用グリーン関数の計算方法の模式図。ソース候補位置の範囲を赤枠で、それを囲む格子セルを★で示す。水色のセルはこの計算において実用グリーン関数を計算したい観測点であり、そのセル内の矢印(→)は計算したい実用グリーン関数の成分を表している。この位置にこの矢印の向きのシングルフォースを与えて波動場を計算する。ソース候補範囲を囲む格子セル(★) の1つ外側のセル(☆) までの範囲(黒枠)のスナップショットを出力する。その際に--snapshot_place=dオプションを付けると青矢印(→↑)で示した成分が出力される。これらを組合せることで★の位置においてシングルフォース3成分、モーメントテンソル6成分を構築できる。例えば★の位置でのシングルフォースやモーメントテンソルは紫色の矢印(→↑) で示した成分を組合せることで構築できる。
Fig. 1. A schematic illustration for the method to compute practical Green’s functions. The spatial extent of candidate source locations is shown by the red rectangle, and grid cells that bound this region are shown by ★. The blue cell represents a station location where the practical Green’s functions are to be computed; the arrow in this cell (→) shows the component of the practical Green’s functions to be computed. Give a single force of this direction at this location to compute a wave field. Output snapshots within 1 cell outside (☆) of the grid cells that bound candidate source locations (★); this range is shown by the black frame. Append --snapshot_place=d option; then, the components shown by brue arrows →↑ are obtained as the snapshots. By combining them, three single force and six moment tensor components at the locations of ★ can be constructed. For example, the single force and moment tensor components at the location of ★ can be constructed from the components shown by purple arrows (→↑).

傾斜変動レートの実用グリーン関数$d\tilde{g}_{nm}^{tilt}(t)/dt$も同様の考え方で計算できる。ソースメカニズムとしてTx, Ty, Tx2, Ty2を選択するほかは速度の実用グリーン関数と同様である。但し、Maeda et al. (2011)において傾斜変動は観測点近傍の5つの格子セルでの値を平均して用いるべきであることが述べられており、そのためには地震波動ソースを観測点近傍の5つの格子セルに 0.2ずつのソース強度で与える必要がある。
Practical tilt-rate Green’s functions can be computed in the same way except that Tx, Ty, Tx2, or Ty2 is chosen for the source mechanism. However, Maeda et al. (2011) recommends that the tilt should be averaged over five grid cells around each station. To realize this, the seismic wave sources should be placed at the five grid cells, each with a source intensity of 0.2.

実用グリーン関数は1つのディレクトリを作成し、その下にトレース別かつ速度・傾斜変動レートの種別ごとのサブディレクトリを作成してその下で計算を行う。
Compute practical Green’s functions under the sub directory for each trace and for each type of velocity or tilt rate under a directory.

winvコマンドでは実用グリーン関数を以下のように用いる。 (\ref{eq.u_n})式の両辺に$s^{green}(t)$をコンボリューションした量を $\tilde{u}_n(t)$とおくと \[\begin{eqnarray} \tilde{u}_n(t) & \equiv & s^{green}(t)∗u_n(t) \nonumber \\ &=& \sum_{m=0}^{M-1} s_m(t)∗\left[ s^{green}(t)∗g_{nm}^{trans}(t)∗i_n^{trans}(t) \right. \nonumber \\ & & \left. +s^{green}(t)∗g_{nm}^{tilt}(t)∗i_n^{tilt}(t) \right] \label{eq.u_n.s_green_convolved} \end{eqnarray}\] となり、(\ref{eq.practical_Green})式を用いて \[\begin{equation} \tilde{u}_n(t)=\sum_{m=0}^{M-1} s_m(t)∗\left[ \tilde{g}_{nm}^{trans}(t)∗i_n^{trans}(t) +\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t) \right] \label{eq.u_n.use_practical} \end{equation}\] と書き直せる。 winvコマンドでは実際には(\ref{eq.u_n})式の代わりに (\ref{eq.u_n.use_practical})式が用いられる。つまり、$s^{green}(t)$を実用グリーン関数からデコンボリューションするのではなく $u_n(t)$の方にコンボリューションする。なお$u_n(t)$に$s^{green}(t)$をコンボシューションする操作はプログラム内で自動で行われるのでユーザが行う必要は無いが、 $s^{green}(t)$の情報をプログラムに与える必要がある。
The winv command uses practical Green’s functions as follows. Convolving $s^{green}(t)$ to the both sides of Eq. (\ref{eq.u_n}) results in (\ref{eq.u_n.s_green_convolved}), which can be arranged as (\ref{eq.u_n.use_practical}) using Eq. (\ref{eq.practical_Green}). The winv command actually uses Eq. (\ref{eq.u_n.use_practical}) instead of (\ref{eq.u_n}); $s^{green}(t)$ is convolved with $u_n(t)$ rather than deconvolved from practical Green’s functions. Users do not need to amnually convolve $s^{green}(t)$ with $u_n(t)$, as the convolution is performed automatically within the program. However, users need to give information on $s^{green}(t)$ to the program.

実用グリーン関数に関するパラメータを下表に示す。
The table below shows parameters for practical Green’s functions.

パラメータ名 Parameter name	意味 Meaning	可能なパラメータ値 Allowed parameter values	デフォルト値 Default value
greendir	実用グリーン関数が保存されているディレクトリ。 A directory in which practical Green’s functions are stored.	ディレクトリパスを表す文字列。 A string that represents a directory path.	green
green_subsubdir	個々のサブディレクトリ内において実用グリーン関数の計算結果が保存されているサブサブディレクトリ名。 waterPMLコマンドを用いて実用グリーン関数を計算した際にパラメータoutput_dirで与えた値である。 A sub-sub directory name for the computation results of practical Green’ functions under each sub directory; it is the value of parameter output_dir of the waterPML command used to compute the practical Green’s functions.	ディレクトリ名(パスを含まない)を表す文字列。 A string that represents a directory name, not including its path.	PML
green_snapname	実用グリーン関数のスナップショットの名前。実用グリーン関数をwaterPMLコマンドを用いて計算した際にスナップショットの設定ファイル内で用いたパラメータsnapnameの値を与える。 The name of snapshots in practical Green’s functions; it is the value of parameter snapname in the configuration file for snapshots for the waterPML command used in the calculation of practical Green’s functions.	ファイル名の一部をなす文字列。 A string used for a part of a file name.	source
green_size	実用グリーン関数の時刻サンプル数。 The number of time samples of practical Green’s functions.	正の整数。 A positive integer.	省略不可 Cannot be omitted
green_t0	実用グリーン関数の先頭時刻(s)。 The beginning time (s) of practical Green’s functions.	実数。 A real number.	0.0
green_dt	実用グリーン関数の時間刻み(s)。 Sampling interval (s) of practical Green’s functions.	正の実数。 A positive real number.	省略不可 Cannot be omitted
stfun_name	$s^{green}(t)$の関数名。 Name of function $s^{green}(t)$.	sequence/timefunc.h で定義されている関数名から選択する。 Choose from the functions defined in sequence/timefunc.h.	pow3-4
stfun_tp	$s^{green}(t)$の1つ目の時定数$\tau_p$(s)。 sequence/timefunc.h での定義に基づく。 The first time constant $\tau_p$ (s) of $s^{green}(t)$, based on the definitions in sequence/timefunc.h.	正の実数。 A positive real number.	省略不可 Cannot be omitted
stfun_ts	$s^{green}(t)$の2つ目の時定数$\tau_s$(s)。 sequence/timefunc.h での定義に基づく。 The second time constant $\tau_s$ (s) of $s^{green}(t)$, based on the definitions in sequence/timefunc.h.	実数。 A real number.	パラメータstfun_tpの値。 The value of parameter stfun_tp.

(4)データとグリーン関数の処理に関するパラメータ (Parameters for processing data and Green’s functions)
(\ref{eq.u_n.use_practical})式の右辺の[ ]内の量を \[\begin{equation} \tilde{g}_{nm}(t)\equiv \tilde{g}_{nm}^{trans}(t)∗i_n^{trans}(t) +\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t) \label{eq.green.sum} \end{equation}\] とおく。この量はプログラム内で以下のように計算される。
Let us introduce $\tilde{g}_{nm}(t)$ (Eq. \ref{eq.green.sum}), which is equal to the quantity in [ ] of the right hand side of Eq. (\ref{eq.u_n.use_practical}). This quantity is computed in the program as follows.

まず第1項の$\tilde{g}_{nm}^{trans}(t)∗i_n^{trans}(t)$については poleとzeroで指定される地震計の応答特性を実用グリーン関数にコンボリューションするだけであり、関数transfer2 を用いて計算される。
The computation of the 1st term $\tilde{g}_{nm}^{trans}(t)∗i_n^{trans}(t)$ only requires the convolution of an instrumental response, specified by poles and zeroes of a seismometer, to practical Green’s functions; this operation is implemented by function transfer2.

第2項の$\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$の計算は以下の手順で行われる。上下成分においては傾斜変動からの寄与は無い($i_n^{tilt}(t)=0$)ものとする。水平成分において、地震計が角度$\tilde{g}_{nm}^{tilt}(t)$だけ傾くと質量$m_s$の地震計には \[\begin{equation} F_n^{gravity}(t) =-m_sg\sin\tilde{g}_{nm}^{tilt}(t) \sim -m_sg\tilde{g}_{nm}^{tilt}(t) \label{eq.gravity} \end{equation}\] の重力が生じる。ここで$g$は鉛直に作用する重力加速度である。傾斜変動は座標軸の正方向が相対的に隆起した場合を正としており、このときの重力の向きは座標軸の負方向であるので$-$を付けた。地震計はこの重力を慣性力と区別できないので、あたかも地震計に(\ref{eq.gravity})式の慣性力が作用した、すなわち \[\begin{equation} a_n^{gravity}(t) =g\tilde{g}_{nm}^{tilt}(t) \label{eq.acceleration.gravity} \end{equation}\] の加速度が生じたようなシグナルを描く。 (\ref{eq.acceleration.gravity})式に等価な変位は \[\begin{equation} u_n^{gravity}(t) =\int_0^t dt’ \int_0^{t’} dt{’}{’} a_n^{gravity}(t{’}{’}) =\int_0^t dt’ \int_0^{t’} dt{’}{’} \left[g\tilde{g}_{nm}^{tilt}(t{’}{’})\right] \label{eq.displacement.gravity} \end{equation}\] であるので、この(\ref{eq.displacement.gravity})式の変位に対する地震計の応答がシグナルとして記録される。そのシグナルとは $u_n^{gravity}(t)∗i_n^{trans(t)}$ であり、これが $\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$ に等しい。すなわち \[\begin{equation} \tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t) =u_n^{gravity}(t)∗i_n^{trans(t)} =\left\{ \int_0^t dt’ \int_0^{t’} dt{’}{’} \left[g\tilde{g}_{nm}^{tilt}(t{’}{’})\right] \right\}∗i_n^{trans(t)} \label{eq.tilt_response} \end{equation}\] である。このことから$\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$は

$\tilde{g}_{nm}^{tilt}(t)$に$g$を掛ける
時間で2回積分する
得られた時系列データにpoleとzeroで指定される地震計の応答特性をコンボリューションする

という3ステップで計算できることが分かる。
The computation of the 2nd term $\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$ uses the procedure explained below. A tilt is assumed to have no contribution to a vertical seismogram ($i_n^{tilt}(t)=0$). Let as consider a horizontal seismogram. If a seismometer inclined by angle $\tilde{g}_{nm}^{tilt}(t)$, a gravitational force of Eq. (\ref{eq.gravity}) exerts to the seismometer, where $g$ is a gravitational acceleration in the vertical direction. The sign $-$ is appended in this equation because a tilt is defined as positive if the ground in the positive side of a coordinate axis uplifted relatively; in this case the gravity works to a negative side. A seismometer cannot distinguish the gravitational force from an inertial force. Therefore, the seismometer records a signal as if an acceleration of Eq. (\ref{eq.acceleration.gravity}), or a displacement of Eq. (\ref{eq.displacement.gravity}), occurred on the ground. Therefore, the seismometer records a signal expressed as $u_n^{gravity}(t)∗i_n^{trans(t)}$, which must be equal to $\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$, giving Eq. (\ref{eq.tilt_response}). This equation indicates that $\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$ can be computed by the following three steps:

multiply $g$ to $\tilde{g}_{nm}^{tilt}(t)$;
integrate the resultant time series data twice; and
convolve an instrumental response, specified by poles and zeroes of a seismometer, to the resultant time series data.

この計算自体はプログラム内で自動で行われるのでユーザが手作業で計算する必要は無い。但し、この計算のためにいくつかのパラメータが必要になり、ユーザはその意味を理解している必要がある(図2)。
These processings are performed automatically in the program; users do not need to manually perform these processings. However, users need to understand several parameters used in these processings (Fig. 2).

図2aはwaterPMLコマンドを用いて計算した実用グリーン関数$\tilde{g}_{nm}^{tilt}(t)$を模式的に表したものである。これは最終時刻よりも前に値が0に収束する程度の長さのものを用意すれば良い。必要以上に長くすると計算に時間がかかるので適切な長さを検討して計算する。この長さを$T^g$とする(図2)。
Fig. 2a schematically shows a practical Green’s function $\tilde{g}_{nm}^{tilt}(t)$ computed by waterPML command. The length of this data should be long enough that the Green’s function converges to zero before the end of the data, but short enough to save the computation time. Let this length be $T^g$ (Fig. 2).

winvコマンド内部ではまず実用グリーン関数の前後にダミーの0を付加して長い時系列データにする(図2b)。その長さは地震計の固有周期よりも十分に長くなければならない。さもないと地震計の応答特性を正しくコンボリューションできないからである。
The winv command first appends dummy zeroes before and after the practical Green’s function to make it enough longer (Fig. 2b) than the natural period of the seismometer; otherwise the convolution of the instrumental response would not be appropriate.

次に、この時系列データに重力加速度を掛けた上で積分が2回行われる(図2c, 図2d)。図2dは$u_n^{gravity}(t)$の時系列データである。このデータに地震計の応答特性をコンボリューションすると図2eの時系列データが得られる。
Next, this time series data is multiplied with the gravitational acceleration and integrated twice (Figs. 2c and 2d). Fig. 2d is a time series data for $u_n^{gravity}(t)$. Convolving it with the instrumental response results in a time series data shown in Fig. 2e.

図2eでは先頭部分に大振幅のシグナルが見られる。これはコンボリューションの計算を行う際に、図2dの時系列データが無限に繰り返されていると仮定されるためであり、図2dの末尾のサンプルと先頭のサンプルの間に存在する大振幅のステップに対する応答が図2eの先頭部分に現れてしまったということである。すなわち、本来は無限の長さを持つはずの$u_n^{gravity}(t)$が有限の長さでカットされていることによる人為的なシグナルである。
A large amplitude signal is prominent at the beginning portion of Fig. 2e, which is a response to a large amplitude step between the final and first samples of the data in Fig. 2d; the convolution assumes that the time series data in Fig. 2d is repeated infinitely. The large signal at the beginning of Fig. 2e is, therefore, an artifact caused by a limited length of $u_n^{gravity}(t)$.

そこで図2fではこの人為的なシグナルを含む時間窓を切り捨てて真のシグナルが卓越する時間窓のみを残している。この図2fが最終的に逆解析に用いられる $\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$ の波形である。
This artificial signal is truncated in Fig. 2f to extract a time window in which true signals are dominant. Fig. 2f is the waveform of $\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$ that is ultimately used in the inversion.

以上の処理手順の中で図2に赤で示した4つの時定数 $T_1^b$, $T_1^a$, $T_2^b$, $T_2^a$ が登場する(上付き添字のbはbefore, aはafterの意)。
These procedures use four time constants $T_1^b$, $T_1^a$, $T_2^b$, $T_2^a$ shown by red in Fig. 2 (the superscript “b” means before, “a” means after).

図2. $\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$ を計算する実際の手順とその中で用いられる時定数の定義。 (a)waterPMLコマンドで計算した$\tilde{g}_{nm}^{tilt}(t)$の (b)前後にダミーの0を付加し、 (c)1回積分し、 (d)更にもう1回積分し、 (e)地震計特性をコンボリューションして (f)人為的なシグナルをカットする。
Fig. 2. Actual steps to compute $\tilde{g}_{nm}^{tilt}(t)∗i_n^{tilt}(t)$ and definitions of time constants used in these procedures. (a) The original $\tilde{g}_{nm}^{tilt}(t)$ computed by the waterPML command. (b) Dummy zeroes are added before and after this data, (c) integrated, (d) again integrated, (e) an instrumental response is convolved, and (f) artificial signals are truncated.

観測波形$u_n(t)$の前後にもダミーの0のデータを付加する(図3)。その目的は実用グリーン関数$\tilde{g}_{nm}(t)$と長さを揃えることである。ユーザは$u_n(t)$の前に付加するダミーの0のデータ長($T_3^b$)を指定することができる。後ろに付加するダミーの0の長さ($T_3^a$)は $u_n(t)$と$\tilde{g}_{nm}(t)$の長さが等しくなるように、すなわち \[\begin{equation} T_3^b+T^u+T_3^a=(T_1^b-T_2^b)+T^g+(T_1^a-T_2^a) \label{eq.T3a.requirement} \end{equation}\] となるように自動的に決定される。
Dummy zeroes are also added before and after the observed waveforms $u_n(t)$ (Fig. 3) to make their lengths equal to those of practical Green’s functions $\tilde{g}_{nm}(t)$. Users can specify the length of dummy zero data to be appended before $u_n(t)$ ((\T_3^b\)); that after $u_n(t)$ ($T_3^a$) is determined automatically to make the lengths of $u_n(t)$ and $\tilde{g}_{nm}(t)$ equal (Eq. \ref{eq.T3a.requirement}).

図3. 観測波形の前後へのダミーデータの付加。 (a)元々の観測波形。パラメータcut_stで指定した日時を先頭、 cut_enで指定した日時を末尾とするデータである。 (b)前後にダミーの0のデータを付加した波形。 $T_3^a$は(\ref{eq.T3a.requirement})式を満たすように自動的に決定される。
Fig. 3. A schematic illustration for adding dummy data before and after the observed data. (a) An original observed waveform. It begins at the date and time specified by parameter cut_st and ends at the date and time specified by parameter cut_en. (b) An waveform with the dummy zero data added before and after the original waveform. The value of $T_3^a$ is determined automatically to satisfy Eq. (\ref{eq.T3a.requirement}).

以上の処理に関するパラメータを下表に示す。
The table below shows the parameters for these processings.

パラメータ名 Parameter name	意味 Meaning	可能なパラメータ値 Allowed parameter values	デフォルト値 Default value
dataseq_list_file	使用する観測データと実用グリーン関数のリストファイル名。 The name of a file that lists the observed data and practical Green’s functions.	ファイル名を表す文字列。 A string that represents a file name. ファイルの書式 (File format)	dataseq.list
N	使用するトレースの数。 The number of traces used.	パラメータMの値以上かつパラメータdataseq_list_fileで指定するファイルの空行・コメントを除いた行数($N_{max}$)以下の正の整数。なお$N<N_{max}$の場合にはパラメータdataseq_list_fileで指定するファイルでの登場順に最初の$N$個の要素ソースが用いられる。 A positive integer greater than or equal to the value of parameter M and less than or equal to the number of lines $N_{max}$ (excluding empty lines and comments) of the file specified by parameter dataseq_list_file. If $N<N_{max}$, only the first $N$ elementary sources (based on the order in the file specified by parameter dataseq_list_file) are used.	$N_{max}$
polezero_dir	地震計の応答特性のファイルが格納されているディレクトリ。 A directory in which files for poles and zeroes of seismometers are stored.	ディレクトリパスを表す文字列。 A string that represents a directory path.	$YMAEDA_OPENTOOL_DIR/winv/share/polezero
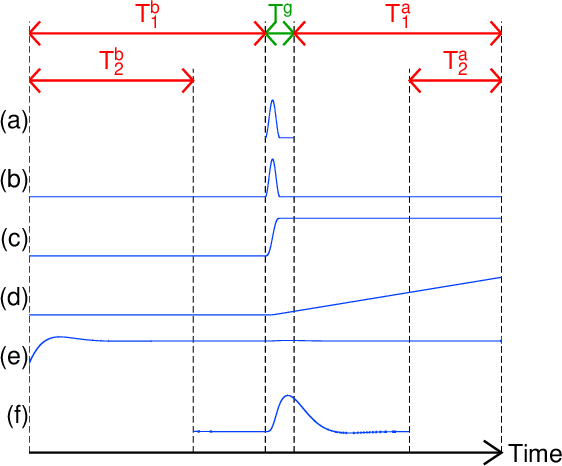
green_zero_before	図2の$T_1^b$の値(s)。 The value of $T_1^b$ (s) in Fig. 2.	正の実数。 A positive real number.	省略不可 Cannot be omitted
green_zero_after	図2の$T_1^a$の値(s)。 The value of $T_1^a$ (s) in Fig. 2.	正の実数。 A positive real number.	省略不可 Cannot be omitted
green_cut_before	図2の$T_2^b$の値(s)。 The value of $T_2^b$ (s) in Fig. 2.	$T_1^b$よりも小さな正の実数。 A positive real number less than $T_1^b$.	省略不可 Cannot be omitted
green_cut_after	図2の$T_2^a$の値(s)。 The value of $T_2^a$ (s) in Fig. 2.	$T_1^a$よりも小さな正の実数。 A positive real number less than $T_1^a$.	省略不可 Cannot be omitted
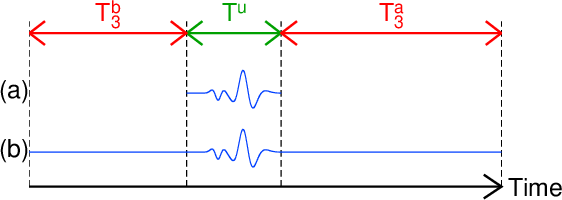
data_zero_before	図3の$T_3^b$の値(s)。 The value of $T_3^b$ (s) in Fig. 3.	正の実数。 $T_3^b+T^u$が図2fのデータ長(\ref{eq.T3a.requirement}式の右辺)以下でなければならない。 A positive real number. The value of $T_3^b+T^u$ must be less than or equal to the time length of the data in Fig. 2f (the right hand side of Eq. \ref{eq.T3a.requirement}).	$T_1^b-T_2^b$

(5)逆解析の手法・条件に関するパラメータ (Parameters for the method and configuration of inversion)
(\ref{eq.green.sum})式を(\ref{eq.u_n.use_practical})式に代入すると \[\begin{equation} \tilde{u}_n(t)=\sum_{m=0}^{M-1} s_m(t)∗\tilde{g}_{nm}(t) \label{eq.u_n.use_practical.simplified} \end{equation}\] という簡単な形になる。 winvコマンドでは逆解析を周波数領域で行う。 (\ref{eq.u_n.use_practical.simplified})式の両辺をフーリエ変換すると \[\begin{equation} \tilde{U}_n(\omega) =S^{green}(\omega)U_n(\omega) =\sum_{m=0}^{M-1} S_m(\omega)\tilde{G}_{nm}(\omega) \label{eq.U_n.use_practical} \end{equation}\] となる。ここで$\omega$は角周波数、 $\tilde{U}_n(\omega)$, $S^{green}(\omega)$, $U_n(\omega)$, $S_m(\omega)$, $\tilde{G}_{nm}(\omega)$ はそれぞれ $\tilde{u}_n(t)$, $s^{green}(t)$, $u_n(t)$, $s_m(t)$, $\tilde{g}_{nm}(t)$ のフーリエスペクトルである。 $S^{green}(\omega)$は与える量、 $U_n(\omega)$は観測データから計算される量、 $\tilde{G}_{nm}(\omega)$は理論計算で求まる量であり、これらを用いて$S_m(\omega)$を求める逆問題となる。 $S_m(\omega)$が求まればこれをフーリエ逆変換することで$s_m(t)$が求まる。
Inserting Eq. (\ref{eq.green.sum}) into (\ref{eq.u_n.use_practical}) reduces to (\ref{eq.u_n.use_practical.simplified}). The winv command performs inversion in the frequency domain. Taking the Fourier transformations for the both side of Eq. (\ref{eq.u_n.use_practical.simplified}) gives Eq. (\ref{eq.U_n.use_practical}), where $\omega$ is an angular frequency and $\tilde{U}_n(\omega)$, $S^{green}(\omega)$, $U_n(\omega)$, $S_m(\omega)$, and $\tilde{G}_{nm}(\omega)$ are the Fourier spectra of $\tilde{u}_n(t)$, $s^{green}(t)$, $u_n(t)$, $s_m(t)$, and $\tilde{g}_{nm}(t)$, respectively. The inverse problem solves for $S_m(\omega)$ from $S^{green}(\omega)$ (which is a given quantity), $U_n(\omega)$ (which is computed from observed data), and $\tilde{G}_{nm}(\omega)$ (which is computed theoretically). A Fourier inverse transformation of $S_m(\omega)$ gives $s_m(t)$.

(\ref{eq.U_n.use_practical})式は線形逆問題の一般的な形 \[\begin{equation} \myvector{d}(\omega)=\myvector{G}(\omega)\myvector{m}(\omega) \label{eq.inverse_problem} \end{equation}\] になっている。ここで \[\begin{equation} \myvector{d}(\omega)\equiv \begin{pmatrix} \tilde{U}_0(\omega) \\ \vdots \\ \tilde{U}_{N-1}(\omega) \end{pmatrix} \hspace{1em} (N\times 1) \label{eq.d} \end{equation}\] はデータベクトル、 \[\begin{equation} \myvector{G}(\omega)\equiv \begin{pmatrix} \tilde{G}_{00}(\omega) & & \cdots \tilde{G}_{0,M-1}(\omega) \\ \vdots & \ddots & \vdots \\ \tilde{G}_{N-1,0}(\omega) & \cdots & \tilde{G}_{N-1,M-1}(\omega) \end{pmatrix} \hspace{1em} (N\times M) \label{eq.G} \end{equation}\] はデータ核、 \[\begin{equation} \myvector{m}(\omega)\equiv \begin{pmatrix} S_0(\omega) \\ \vdots \\ S_{M-1}(\omega) \end{pmatrix} \hspace{1em} (M\times 1) \label{eq.m} \end{equation}\] はモデルベクトルである。角周波数$\omega$毎に独立な逆問題となるので行列サイズが小さく、時間領域で解くよりも高速になる(Auger et al. 2006)。
Eq. (\ref{eq.U_n.use_practical}) has a form of a general linear inverse problem (Eq. \ref{eq.inverse_problem}), where $\myvector{d}(\omega)$ (Eq. \ref{eq.d}; is a data vector, $\myvector{G}(\omega)$ (Eq. \ref{eq.G}; is a data kernel, and $\myvector{m}(\omega)$ (Eq. \ref{eq.m}; is a model vector. This inverse problem can be solved for each angular frequency $\omega$ independently, thereby realizing a smaller matrix size and thus a faster computation than solving in time domain (Auger et al. 2006).

ymaeda_opentoolsでは実数行列のみを扱える関係上、実際の取り扱いはもう少し複雑である。以下では行列の下付き添字の$\myvector{_r}$が実部を、 $\myvector{_i}$が虚部を表すものとする。 (\ref{eq.inverse_problem})式を実部と虚部に分けると \[\begin{eqnarray} \myvector{d_r}(\omega)+\myvector{d_i}(\omega)i &=& \left[\myvector{G_r}(\omega)+\myvector{G_i}(\omega)i\right] \left[\myvector{m_r}(\omega)+\myvector{m_i}(\omega)i\right] \nonumber \\ &=& \left[ \myvector{G_r}(\omega)\myvector{m_r}(\omega) -\myvector{G_i}(\omega)\myvector{m_i}(\omega) \right] +\left[ \myvector{G_i}(\omega)\myvector{m_r}(\omega) \myvector{G_r}(\omega)\myvector{m_i}(\omega) \right]i \label{eq.inverse_problem.real_imag} \end{eqnarray}\] となり、実部同士、虚部同士を比較すれば \[\begin{equation} \begin{pmatrix} \myvector{d_r}(\omega) \\ \myvector{d_i}(\omega) \end{pmatrix} = \begin{pmatrix} \myvector{G_r}(\omega) & -\myvector{G_i}(\omega) \\ \myvector{G_i}(\omega) & \myvector{G_r}(\omega) \end{pmatrix} \begin{pmatrix} \myvector{m_r}(\omega) \\ \myvector{m_i}(\omega) \end{pmatrix} \label{eq.inverse_problem.real_matrix} \end{equation}\] となる。 \[\begin{equation} \myvector{\hat{d}}(\omega)\equiv \begin{pmatrix} \myvector{d_r}(\omega) \\ \myvector{d_i}(\omega) \end{pmatrix} \hspace{1em} (2N\times 1) \label{eq.d_hat} \end{equation}\] \[\begin{equation} \myvector{\hat{G}}(\omega)\equiv \begin{pmatrix} \myvector{G_r}(\omega) & -\myvector{G_i}(\omega) \\ \myvector{G_i}(\omega) & \myvector{G_r}(\omega) \end{pmatrix} \hspace{1em} (2N\times 2M) \label{eq.G_hat} \end{equation}\] \[\begin{equation} \myvector{\hat{m}}(\omega)\equiv \begin{pmatrix} \myvector{m_r}(\omega) \\ \myvector{m_i}(\omega) \end{pmatrix} \hspace{1em} (2M\times 1) \label{eq.m_hat} \end{equation}\] とおいて \[\begin{equation} \myvector{\hat{d}}(\omega)= \myvector{\hat{G}}(\omega)\myvector{\hat{m}}(\omega) \label{eq.inverse_problem.hat} \end{equation}\] を得る。 (\ref{eq.inverse_problem.hat})式が実際に解析に用いる式である。
The actual treatment is some more complicated because ymaeda_opentools can treat only the matrices composed of real numbers. Below, subscripts $\myvector{_r}$ and $\myvector{_i}$ represent real and imaginary parts of a matrix, respectively. Eq. (\ref{eq.inverse_problem}) can be decomposed into real and imaginary parts as (\ref{eq.inverse_problem.real_imag}). A comparison of real and imaginary parts of the both sides gives Eq. (\ref{eq.inverse_problem.real_matrix}), which can further be arranged as (\ref{eq.inverse_problem.hat}), where the matrices are defined as Eqs. (\ref{eq.d_hat})-(\ref{eq.m_hat}). Eq. (\ref{eq.inverse_problem.hat}) is indeed used in the analysis.

winvコマンドでは(\ref{eq.inverse_problem.hat})式の解を特異値分解で求める。以下では簡単のため$\omega$を省略する。固有値問題 \[\begin{equation} \begin{pmatrix} \myvector{0} & \myvector{\hat{G}} \\ \myvector{\hat{G}}^T & \myvector{0} \end{pmatrix} \begin{pmatrix} \myvector{u_i} \\ \myvector{v_i} \end{pmatrix} =\lambda_i \begin{pmatrix} \myvector{u_i} \\ \myvector{v_i} \end{pmatrix} \label{eq.G_enlarged.eigen_problem} \end{equation}\] を考える。ここで上付き添字の$^T$は行列の転置を表す。 $\myvector{u_i}$は$2N\times 1$、$\myvector{v_i}$は$2M\times 1$である。 $\lambda_i$は行列$\myvector{\hat{G}}$の特異値と呼ばれ、最大$2M$個がノンゼロである。これらを降順に並べ替えて $\lambda_0\geq\lambda_1\geq\cdots\geq\lambda_{2P-1}\geq \lambda_{2P}=\lambda_{2P+1}=\cdots =\lambda_{2N-1}=0$ とする。ここで$2P(\leq 2M)$はノンゼロ特異値の個数である (複素行列を用いる取り扱いであればノンゼロ特異値の個数は$P$個であるところ、複素数を2つの実数で表している関係でノンゼロ特異値の個数が$2P$個になる)。 \[\begin{equation} \myvector{U}\equiv \begin{pmatrix} \myvector{u_0} & \cdots & \myvector{u_{2N-1}} \end{pmatrix} \hspace{1em} (2N\times 2N) \label{eq.U} \end{equation}\] \[\begin{equation} \myvector{V}\equiv \begin{pmatrix} \myvector{v_0} & \cdots & \myvector{v_{2M-1}} \end{pmatrix} \hspace{1em} (2M\times 2M) \label{eq.V} \end{equation}\] \[\begin{equation} \myvector{\Lambda}\equiv \begin{pmatrix} \lambda_0 & 0 & \cdots & 0 \\ 0 & \lambda_1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \lambda_{2M-1} \\ 0 & \cdots & \cdots & 0 \\ \vdots & & & \vdots \\ 0 & \cdots & \cdots & 0 \end{pmatrix} \hspace{1em} (2N\times 2M) \label{eq.Lambda} \end{equation}\] およびこれらの部分行列 \[\begin{equation} \myvector{U_P}\equiv \begin{pmatrix} \myvector{u_0} & \cdots & \myvector{u_{2P-1}} \end{pmatrix} \hspace{1em} (2N\times 2P) \label{eq.U_P} \end{equation}\] \[\begin{equation} \myvector{V_P}\equiv \begin{pmatrix} \myvector{v_0} & \cdots & \myvector{v_{2P-1}} \end{pmatrix} \hspace{1em} (2M\times 2P) \label{eq.V_P} \end{equation}\] \[\begin{equation} \myvector{\Lambda_P}\equiv \begin{pmatrix} \lambda_0 & 0 & \cdots & 0 \\ 0 & \lambda_1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \lambda_{2P-1} \end{pmatrix} \hspace{1em} (2P\times 2P) \label{eq.Lambda_P} \end{equation}\] を定義すると \[\begin{equation} \myvector{\hat{G}} =\myvector{U}\myvector{\Lambda}\myvector{V}^T =\myvector{U_P}\myvector{\Lambda_P}\myvector{V_P}^T \label{eq.SVD} \end{equation}\] が成り立ち、この関係は$\myvector{\hat{G}}$の特異値分解と呼ばれる(Menke 1989)。 (\ref{eq.SVD})を(\ref{eq.inverse_problem.hat})に代入すると \[\begin{equation} \myvector{\hat{d}}= \myvector{U_P}\myvector{\Lambda_P}\myvector{V_P}^T\myvector{\hat{m}} \label{eq.inverse_problem.SVD} \end{equation}\] となり、その解は \[\begin{equation} \myvector{\hat{m}}= \myvector{V_P}\myvector{\Lambda_P}^{-1}\myvector{U_P}^T\myvector{\hat{d}} \label{eq.solution.SVD} \end{equation}\] となる。winvコマンドでは(\ref{eq.solution.SVD})式を解として採用する。
The winv command solves Eq. (\ref{eq.inverse_problem.hat}) using a singular value decomposition. Below, $\omega$ is omitted for simplicity. Let us consider an eigen value problem expressed as Eq. (\ref{eq.G_enlarged.eigen_problem}), where a superscript $^{T}$ denotes the transpose of a matrix; $\myvector{u_i}$ is $2N\times 1$ and $\myvector{v_i}$ is $2M\times 1$. There are at maximum $2M$ non-zero $\lambda_i$, which are called singular values of a matrix $\myvector{\hat{G}}$. Let us sort them in a descending order as: $\lambda_0\geq\lambda_1\geq\cdots\geq\lambda_{2P-1}\geq \lambda_{2P}=\lambda_{2P+1}=\cdots =\lambda_{2N-1}=0$, where $2P(\leq 2M)$ is the number of non-zero singular values; the number would have been $P$ if complex matrices were used directory, but it is $2P$ because each complex number is expressed by two real numbers. Let us define matrices $\myvector{U}$, $\myvector{V}$, and $\myvector{\Lambda}$ (Eqs. \ref{eq.U}-\ref{eq.Lambda}) and their partial matrices (Eqs. \ref{eq.U_P}-\ref{eq.Lambda_P}). Eq. (\ref{eq.SVD}) holds for these matrices; this relation is called a singular value decomposition of $\myvector{\hat{G}}$ (Menke 1989). Inserting Eq. (\ref{eq.SVD}) into (\ref{eq.inverse_problem.hat}) results in (\ref{eq.inverse_problem.SVD}), and the solution of it is given as Eq. (\ref{eq.solution.SVD}). The winv command adopts this solution.

比較的短周期のシグナル(LPイベント等)においては波形逆解析の結果は仮定する地下構造の影響を強く受けるとされる (Bean et al., 2008)。その原因として仮定する地震波速度と真の地震波速度の差異に起因する合成波形と観測波形の位相ずれが考えられ、原理的には波形ではなくエンベロープを用いて残差を評価すれば逆解析が成功することが期待される。このような考えのもと、winvコマンドでは波形の代わりにヒルベルトエンベロープを用いる逆解析を実装してみた (但し、手法の開発・検証以外での同手法の利用は非推奨である)。ヒルベルトエンベロープを用いる逆解析は以下のように定式化される。 $\tilde{u}_n(t)$のヒルベルト変換を$\tilde{u}_n^H(t)$、 $\tilde{g}_{nm}(t)$のヒルベルト変換を$\tilde{g}_{nm}^H(t)$、それらのフーリエスペクトルを $\tilde{U}_n^H(\omega)$, $\tilde{G}_{nm}^H(\omega)$ とおくと、ヒルベルト変換の定義により \[\begin{equation} \tilde{U}_n^H(\omega)=i sign(\omega)\tilde{U}_n(\omega) \label{eq.U_n.hilbert} \end{equation}\] \[\begin{equation} \tilde{G}_{nm}^H(\omega)=i sign(\omega)\tilde{G}_{nm}(\omega) \label{eq.G_nm.hilbert} \end{equation}\] が成り立つ。ここで$sign$は符号を表す。 (\ref{eq.U_n.use_practical})(\ref{eq.U_n.hilbert})(\ref{eq.G_nm.hilbert})式より \[\begin{eqnarray} \tilde{U}_n^H(\omega) &=& i sign(\omega)\tilde{U}_n(\omega) \nonumber \\ &=& i sign(\omega) \sum_{m=0}^{M-1}S_m(\omega)\tilde{G}_{nm}(\omega) \nonumber \\ &=& \sum_{m=0}^{M-1}S_m(\omega)\tilde{G}_{nm}^H(\omega) \label{eq.U_n.use_practical.hilbert} \end{eqnarray}\] であるので \[\begin{equation} \tilde{u}_n^H(t) =\sum_{m=0}^{M-1}s_m(t)∗\tilde{g}_{nm}^H(t) \label{eq.u_n.use_practical.hilbert} \end{equation}\] という関係式が得られる。 $\tilde{u}_n(t)$, $\tilde{g}_{nm}(t)$のヒルベルトエンベロープはそれぞれ \[\begin{equation} \tilde{u}_n^e(t)\equiv\sqrt{\tilde{u}_n(t)^2+\tilde{u}_n^H(t)^2} \label{eq.u_n.envelope} \end{equation}\] \[\begin{equation} \tilde{g}_{nm}^e(t)\equiv\sqrt{\tilde{g}_{nm}(t)^2+\tilde{g}_{nm}^H(t)^2} \label{eq.g_nm.envelope} \end{equation}\] と定義されるので (\ref{eq.u_n.use_practical.simplified}) (\ref{eq.u_n.use_practical.hilbert}) 式より \[\begin{eqnarray} \tilde{u}_n^e(t)^2 &=& \tilde{u}_n(t)^2+\tilde{u}_n^H(t)^2 \nonumber \\ &=& \left[\sum_{m=0}^{M-1}s_m(t)∗\tilde{g}_{nm}(t)\right]^2 +\left[\sum_{m=0}^{M-1}s_m(t)∗\tilde{g}_{nm}^H(t)\right]^2 \nonumber \\ &=& \left[\sum_{m=0}^{M-1}\int_{-\infty}^{\infty} s_m(\tau)\tilde{g}_{nm}(t-\tau)d\tau\right] \left[\sum_{m’=0}^{M-1}\int_{-\infty}^{\infty} s_{m’}(\tau’)\tilde{g}_{nm’}(t-\tau’) d\tau’\right] \nonumber \\ & & +\left[\sum_{m=0}^{M-1}\int_{-\infty}^{\infty} s_m(\tau)\tilde{g}_{nm}^H(t-\tau)d\tau\right] \left[\sum_{m’=0}^{M-1}\int_{-\infty}^{\infty} s_{m’}(\tau’)\tilde{g}_{nm’}^H(t-\tau’) d\tau’\right] \nonumber \\ &=& \sum_{m=0}^{M-1} \sum_{m’=0}^{M-1} \int_{-\infty}^{\infty}d\tau \int_{-\infty}^{\infty}d\tau’ s_m(\tau)s_{m’}(\tau’) \tilde{g}_{nm}(t-\tau)\tilde{g}_{nm’}(t-\tau’) \nonumber \\ & & +\sum_{m=0}^{M-1} \sum_{m’=0}^{M-1} \int_{-\infty}^{\infty}d\tau \int_{-\infty}^{\infty}d\tau’ s_m(\tau)s_{m’}(\tau’) \tilde{g}_{nm}^H(t-\tau)\tilde{g}_{nm’}^H(t-\tau’) \nonumber \\ &=& \sum_{m=0}^{M-1} \sum_{m’=0}^{M-1} \int_{-\infty}^{\infty}d\tau \int_{-\infty}^{\infty}d\tau’ s_m(\tau)s_{m’}(\tau’) \nonumber \\ & & \left[ \tilde{g}_{nm}(t-\tau)\tilde{g}_{nm’}(t-\tau’) +\tilde{g}_{nm}^H(t-\tau)\tilde{g}_{nm’}^H(t-\tau’) \right] \label{eq.envelope_inversion.exact} \end{eqnarray}\] となる。右辺の被積分関数について異なる時刻間や異なる要素ソース間に相関は無いと仮定して被積分関数に$\delta_{mm’}\delta(\tau-\tau’)$を掛けると \[\begin{eqnarray} \tilde{u}_n^e(t)^2 &\sim& \sum_{m=0}^{M-1} \sum_{m’=0}^{M-1} \int_{-\infty}^{\infty}d\tau \int_{-\infty}^{\infty}d\tau’ s_m(\tau)s_{m’}(\tau’) \nonumber \\ & & \left[ \tilde{g}_{nm}(t-\tau)\tilde{g}_{nm’}(t-\tau’) +\tilde{g}_{nm}^H(t-\tau)\tilde{g}_{nm’}^H(t-\tau’) \right]\delta_{mm’}\delta(\tau-\tau’) \nonumber \\ &=& \sum_{m=0}^{M-1}\int_{-\infty}^{\infty}d\tau s_m(\tau)s_m(\tau) \nonumber \\ & & \left[ \tilde{g}_{nm}(t-\tau)\tilde{g}_{nm}(t-\tau) +\tilde{g}_{nm}^H(t-\tau)\tilde{g}_{nm}^H(t-\tau) \right] \nonumber \\ &=& \sum_{m=0}^{M-1}\int_{-\infty}^{\infty}d\tau s_m(\tau)^2 \left[ \tilde{g}_{nm}(t-\tau)^2+\tilde{g}_{nm}^H(t-\tau)^2 \right] \nonumber \\ &=& \sum_{m=0}^{M-1}\int_{-\infty}^{\infty}d\tau s_m(\tau)^2\tilde{g}_{nm}^e(t-\tau)^2 \nonumber \\ &=& \sum_{m=0}^{M-1}s_m(t)^2∗\tilde{g}_{nm}^e(t)^2 \label{eq.envelope_inversion.use} \end{eqnarray}\] となる。winvコマンドにおいて、エンベロープを用いる逆解析はこの(\ref{eq.envelope_inversion.use})式を用いて行う。すなわち$\tilde{u}_n(t)$の代わりに$\tilde{u}_n^e(t)^2$、 $\tilde{g}_{nm}(t)$の代わりに$\tilde{g}_{nm}^e(t)^2$ を使用し、$s_m(t)^2$を求める逆解析となる。 (\ref{eq.envelope_inversion.exact})式を (\ref{eq.envelope_inversion.use})式で近似する理論的裏付けが不十分であり、実際のデータを用いた検証も行っていない。そのためエンベロープを用いる逆解析は実際のソース解析のためではなく手法の検証目的でのみ用いるべきである。
For relatively short-period signals (e.g., LP events), results of waveform inversion are significantly affected by an assumed subsurface structure (e.g., Bean et al., 2008). This is probably because of mismatched phases between synthetic and observed waveforms caused by assumed and actural subsurface velocity structures. Therefore, it is likely that inversion of relatively short-period signals better succeeds by a use of envelopes instead of waveforms for computation of residuals. Based on this idea, the winv command implemented inversion using Hilbert envelopes instead of waveforms; however, use of this option is discouraged except for a purpose of development and examination of the method. Inversion using Hilbert envelopes is formulated as follows. Let $\tilde{u}_n^H(t)$ and $\tilde{g}_{nm}^H(t)$ be the Hilbert transformations of $\tilde{u}_n(t)$ and $\tilde{g}_{nm}(t)$, respectively, and $\tilde{U}_n^H(\omega)$ and $\tilde{G}_{nm}^H(\omega)$ be their Fourier spectra. The definition of a Hilbert transformation gives Eqs. (\ref{eq.U_n.hilbert}) and (\ref{eq.G_nm.hilbert}), where $sign$ represents a sign. Eqs. (\ref{eq.U_n.use_practical}), (\ref{eq.U_n.hilbert}), and (\ref{eq.G_nm.hilbert}) gives (\ref{eq.U_n.use_practical.hilbert}), and thus (\ref{eq.u_n.use_practical.hilbert}). Hilbert envelopes of $\tilde{u}_n(t)$ and $\tilde{g}_{nm}(t)$ are defined as (\ref{eq.u_n.envelope}) and (\ref{eq.g_nm.envelope}), respectively. Therefore, from Eqs. (\ref{eq.u_n.use_practical.simplified}) and (\ref{eq.u_n.use_practical.hilbert}), we obtain Eq. (\ref{eq.envelope_inversion.exact}). Let us assume that the integrand of the right hand side of this equation is not correlated between different times and different elementary sources. Based on this assumption, multiply $\delta_{mm’}\delta(\tau-\tau’)$ with the integrand. The result is Eq. (\ref{eq.envelope_inversion.use}) The winv command uses this equation for the enveloped-based inversion; $\tilde{u}_n^e(t)^2$ and $\tilde{g}_{nm}^e(t)^2$ are used instead of $\tilde{u}_n(t)$ and $\tilde{g}_{nm}(t)$, respectively, and the solution is interpreted as $s_m(t)^2$. Note that the approximation of Eq. (\ref{eq.envelope_inversion.exact}) by (\ref{eq.envelope_inversion.use}) is just an assumption, without tight theoretical basis. Also note that I have not examined this approach. Therefore, the envelope-based inversion by the winv command should be used only for a porpose of examination of the method, and should not be used for the source analysis of an actual signal without the examination.

逆解析に関するパラメータを下表に示す。
The table below shows parameters for inversion.

パラメータ名 Parameter name	意味 Meaning	可能なパラメータ値 Allowed parameter values	デフォルト値 Default value
threshold	特異値$\lambda_i=0$と見なすための最大特異値との比$\lambda_i/\lambda_0$の閾値。数値計算の丸め誤差によって本当は0である特異値がノンゼロになる場合がある。そこで、比$\lambda_i/\lambda_0$がこの閾値よりも小さい場合、 $\lambda_i=0$と見なす。 A threshold value for a ratio $\lambda_i/\lambda_0$ (a ratio of a singular value to its maximum) to regard $\lambda_i$ to be 0 considering a rounding error in numerical computation.	1.0よりも小さな正の実数。 A positive real number less than 1.0.	0.01
envelope	逆解析に波形のエンベロープを使用するか否かの選択。 A choice of whether to use the envelopes of waveforms for the inversion or not.	no 普通の時系列データ(速度波形や変位波形)を用いて逆解析を行う。 Use normal time series data (velocity or displacement waveforms) for inversion. hilbert 波形のヒルベルトエンベロープの2乗を用いて逆解析を行う。 Use the square of hilbert envelopes of the waveforms for inversion.	no

(6)グリッドサーチに関するパラメータ (Parameters for grid searches)
逆解析で求めるのは要素ソースの震源時間関数$s_m(t)$のみであり、ソース位置や(\ref{eq.source.F})(\ref{eq.source.M})式の $F_p^{(m)}$, $M_{pq}^{(m)}$ ($p,q=x,y,z$) はユーザが与える(仮定する)。ソース位置が不明な場合、ソース位置を仮定した逆解析をソース位置の候補の数だけ繰り返し、その中から観測波形と合成波形の残差が最小になるソース位置を採用する(グリッドサーチ)。 $F_p^{(m)}$, $M_{pq}^{(m)}$についても例えば(\ref{eq.Nakano.M})式の$\theta$, $\phi$のように発震機構パラメータを含んだ数式で与え、最適な発震機構パラメータをグリッドサーチで求めることができる。
The inversion is applied only to the source time functions $s_m(t)$ of elementary sources. The source location and $F_p^{(m)}$ and $M_{pq}^{(m)}$ ($p,q=x,y,z$) in Eqs. (\ref{eq.source.F}) and (\ref{eq.source.M}) are given (assumed) by the user. If the source location is unknown, inversion for an assumed source location is repeated for every candidate source location, and the location that minimized the residual between observed and synthetic waveforms is adopted as the optimal source location; this approach is called a grid search. Optimal $F_p^{(m)}$ and $M_{pq}^{(m)}$ can also be investigated by expressing them as equations that include focal mechanism parameters, like $\theta$ and $\phi$ in Eq. (\ref{eq.Nakano.M}), and perform grid searches to estimate the optimal focal mechanism parameters.

winvコマンドでは残差を以下のように計算する。 $u_n(t)$に対応する観測波形を$u_n^{obs}(t)$、逆解析で求めた$s_m(t)$を用いて(\ref{eq.u_n})式により計算される合成波形を \[\begin{equation} u_n^{syn}(t)= \sum_{m=0}^{M-1} s_m(t)∗\left[ g_{nm}^{trans}(t)∗i_n^{trans}(t) +g_{nm}^{tilt}(t)∗i_n^{tilt}(t) \right] \label{eq.u_n_syn} \end{equation}\] とする。なお速度波形を用いる場合には変位を速度で、実用グリーン関数をその導関数で読み替えるものとする。これらの波形に対して共通のローパスフィルターを掛けた波形を $u_n^{obs,lp}(t)$, $u_n^{syn,lp}(t)$ として、winvコマンドのグリッドサーチでは \[\begin{equation} E\equiv \sqrt{\frac{\sum_{n=0}^{N-1}\int_{t_{min}}^{t_{max}} \left[u_n^{obs,lp}(t)-u_n^{syn,lp}(t)\right]^2 dt} {\sum_{n=0}^{N-1}\int_{t_{min}}^{t_{max}} \left[u_n^{obs,lp}(t)\right]^2 dt}} \label{eq.residual} \end{equation}\] を残差として用いる。ここで$t_{min}$, $t_{max}$はユーザが指定する時刻である。この$E$を最小にするソース位置とパラメータを探索する。
The winv command computes the residual as follows. Let $u_n^{obs}(t)$ be an observed waveform corresponding to $u_n(t)$, and $u_n^{syn}(t)$ be a synthetic waveform computed by Eq. (\ref{eq.u_n}) with the solution $s_m(t)$ (i.e., Eq. \ref{eq.u_n_syn}). In case of using velocity waveforms, replace a displacement with a velocity and a practical Green’s function with a derivative of it in the following discussion. Let $u_n^{obs,lp}(t)$ and $u_n^{syn,lp}(t)$ be low-passed waveforms of $u_n^{obs}(t)$ and $u_n^{syn}(t)$, respectively. Eq. (Eq. \ref{eq.residual}) is the definition of the residual for the grid searches in winv command, where $t_{min}$ and $t_{max}$ are times specified by the user. The optimal source location and parameters that minimize this $E$ are searched.

残差の計算に関して補足する。以下では観測波形を用いて計算される量を上付き添字の$^{obs}$を付けて表す。例えば$u_n^{obs}(t)$のフーリエスペクトルは$U_n^{obs}(\omega)$、これに$S^{green}(\omega)$を掛けたものは$\tilde{U}_n^{obs}(\omega)$、これを用いて(\ref{eq.d})(\ref{eq.d_hat})式により構成される観測データベクトルは \[\begin{equation} \myvector{\hat{d}^{obs}}(\omega)\equiv \begin{pmatrix} Re\left[\tilde{U}_0^{obs}(\omega)\right] \\ \vdots \\ Re\left[\tilde{U}_{N-1}^{obs}(\omega)\right] \\ Im\left[\tilde{U}_0^{obs}(\omega)\right] \\ \vdots \\ Im\left[\tilde{U}_{N-1}^{obs}(\omega)\right] \end{pmatrix} \label{eq.d_obs} \end{equation}\] のように表す。ここで$Re$は実部、$Im$は虚部を表す。合成波形に関する量にも同様に上付き添字の$^{syn}$を付けて表す。逆解析自体は周波数毎に独立に行われ、モデルベクトルは(\ref{eq.solution.SVD})式に基づいて \[\begin{equation} \myvector{\hat{m}^{est}}(\omega)= \myvector{V_P}(\omega) \myvector{\Lambda_P}(\omega)^{-1} \myvector{U_P}(\omega)^{T} \myvector{\hat{d}^{obs}}(\omega) \label{eq.m_est} \end{equation}\] と計算される。このモデルベクトル$\myvector{\hat{m}^{est}}(\omega)$に基づいて震源時間関数のフーリエスペクトル$S_m^{est}(\omega)$が構成され、これをフーリエ逆変換することで震源時間関数$s_m^{est}(t)$が得られる。通常の逆解析の枠組みでは合成データベクトルは \[\begin{equation} \myvector{\hat{d}^{syn}}(\omega)\equiv \myvector{\hat{G}}(\omega)\myvector{\hat{m}^{est}}(\omega) \label{eq.d_syn} \end{equation}\] と定義され、観測データベクトルと合成データベクトルの残差は \[\begin{equation} E(\omega)\equiv \sqrt{\frac{\left|\myvector{\hat{d}^{obs}}(\omega) -\myvector{\hat{d}^{syn}}(\omega)\right|^2} {\left|\myvector{\hat{d}^{obs}}(\omega)\right|^2}} =\sqrt{\frac{\sum_{n=0}^{N-1}\left| \tilde{U}_n^{obs}(\omega)-\tilde{U}_n^{syn}(\omega) \right|^2} {\sum_{n=0}^{N-1}\left|\tilde{U}_n^{obs}(\omega)\right|^2}} \label{eq.residual.freq} \end{equation}\] と計算される。この$E(\omega)$ように周波数に依存する残差を用いたのでは最適なソース位置や発震機構パラメータが周波数毎に異なってしまうので都合が悪い。時間領域の波形に直した上で(\ref{eq.residual})式によって残差を計算するのはこのような理由からである。インパルス応答としての真のグリーン関数のデータは存在しないので $u_n^{syn}(t)$の計算に(\ref{eq.u_n_syn})式を直接用いることはできない。そこで実際には$\myvector{\hat{d}^{syn}}(\omega)$を用いて $\tilde{U}_n^{syn}(\omega)$を構成し、これを$S^{green}(\omega)$で割ることで$U_n^{syn}(\omega)$を求め、そのフーリエ逆変換によって$u_n^{syn}(t)$を得る。周波数毎に独立に逆解析を行う影響で $s_m^{est}(t)$や$u_n^{syn}(t)$の波形には高周波の振動成分が多く含まれる場合があり、その影響を低減するために(\ref{eq.residual})式ではローパスフィルターを掛けた波形を用いている。
Additional remarks are needed for the computation of residual. Below, a superscript $^{obs}$ indicates quantities computed from observed waveforms. For example, the Fourier spectrum of $u_n^{obs}(t)$ is expressed as $U_n^{obs}(\omega)$; the spectrum multiplied by $S^{green}(\omega)$ is expressed as $\tilde{U}_n^{obs}(\omega)$; and the data vector constructed using Eqs. (\ref{eq.d}) and (\ref{eq.d_hat}) with this spectrum is expressed as Eq. (\ref{eq.d_obs}), where $Re$ and $Im$ indicates real and imaginary parts, respectively. In the same manner, a superscript $^{syn}$ indicates quantities for synthetic waveforms. The inversion analysis is performed for each frequency independently, and the model vector is calculated as Eq. (\ref{eq.m_est}). From this model vector $\myvector{\hat{m}^{est}}(\omega)$, the Fourier spectra of source time functions $S_m^{est}(\omega)$ are constructed, and the inverse Fourier transformation of them gives the source time functions $s_m^{est}(t)$. Following the standard framework of inverse problem, a synthetic data vector is defined as Eq. (\ref{eq.d_syn}), and the residual between observed and synthetic data vectors is computed as Eq. (\ref{eq.residual.freq}). This $E(\omega)$, which depends on frequency, is inconvenient to determine the optimal source location and focal mechanism parameters as they would also depend on frequency. This is the reason why the residual is defined in the time domain as Eq. (\ref{eq.residual}). Note that $u_n^{syn}(t)$ cannot be directly computed from Eq. (\ref{eq.u_n_syn}) because we do not have true Green’s functions (impulse responses). Instead, $u_n^{syn}(t)$ is computed by constituting the spectra $\tilde{U}_n^{syn}(\omega)$ from $\myvector{\hat{d}^{syn}}(\omega)$, dividing the spectra by $S^{green}(\omega)$ to derive $U_n^{syn}(\omega)$, and performing the Fourier inverse transformation to obtain $u_n^{syn}(t)$. Low-passed waveforms are used in Eq. (\ref{eq.residual}) to reduce high-frequency oscillations that are often contained in $s_m^{est}(t)$ and $u_n^{syn}(t)$ because of the independent inversion for each frequency.

グリッドサーチに関するパラメータ (残差計算のためのローパスフィルターや時間窓のパラメータを含む) を下表に示す。なお 時刻の原点(0)はパラメータcut_stで与えた日時 とする。
Parameters for grid searches, including parameters for the low-pass filter and time window for computation of residuals, are listed in the table below. The time origin (0) is the date and time given by parameter cut_st.

パラメータ名 Parameter name	意味 Meaning	可能なパラメータ値 Allowed parameter values	デフォルト値 Default value
source_location_min	ソース位置のサーチ範囲の下限。 The lower limit of the search range for the source location.	$x$, $y$, $z$座標のサーチ範囲の下限(m)をカンマ(,)で区切って並べた文字列。座標は整数でなければならない。 A string composed of the lower limits of the search ranges of $x$-, $y$-, and $z$-components (m). Separate the coordinates by commas (,). The coordinates must be given in integers.	省略不可 Cannot be omitted
source_location_max	ソース位置のサーチ範囲の上限。 The upper limit of the search range for the source location.	$x$, $y$, $z$座標のサーチ範囲の上限(m)をカンマ(,)で区切って並べた文字列。上限は下限以上でなければならない。また座標は整数でなければならない。 A string composed of the upper limits of the search ranges of $x$-, $y$-, and $z$-components (m). Separate the coordinates by commas (,). The upper limit must be greater than or equal to the lower limit. The coordinates must be given in integers.	省略不可 Cannot be omitted
source_location_inc	ソース位置のサーチの間隔。 Intervals of the search for the source location.	$x$, $y$, $z$座標のサーチ間隔(m)をカンマ(,)で区切って並べた文字列。間隔は正の整数であってかつ上限と下限の差の約数でなければならない。 A string composed of the intervals (m) of the searches in $x$-, $y$-, and $z$-directions. Separate the intervals in the three directions by commas (,). The interval in each direction must be a positive integer and must be a divisor of the difference between the upper and lower limits of the search range.	省略不可 Cannot be omitted
zminmax_reverse	ソース位置のグリッドサーチを浅い($z$が大きい)側から行うか否か。計算の最終結果には影響しないが、時間のかかる計算の途中段階で浅い場所での結果を確認したいか、深い場所での結果を確認したいかに応じて選択する。 A choice of whether to perform a grid search for the source location from shallower (larger $z$) side or not. This choice does not affect the final result; however, the choice affects whether the user can look at the results for shallow or deep candidate source locations during a computation that takes time.	yes 浅い側から行う。 Perform a grid search from a shallower side. no Perform a grid search from a deeper side.	yes
residual_lp_fc	グリッドサーチにおいて残差の評価に用いるローパスフィルターのコーナー周波数(Hz)。 The corner frequency (Hz) of a low-pass filter used in the evaluation of residuals in a grid search.	正の実数。 A positive real number.	省略不可 Cannot be omitted
residual_lp_n	グリッドサーチにおいて残差の評価に用いるローパスフィルターの極の数。 The number of poles of a low-pass filter used in the evaluation of residuals in a grid search.	正の偶数。 A positive even number.	2
residual_tmin	グリッドサーチにおいて残差の計算に用いる時間窓の先頭時刻$t_{min}$(s)。なおパラメータcut_stで与えた日時を時刻$t=0$とする。 The beginning of a time window, $t_{min}$ (s), used for the computation of residuals in a grid search. The time origin ($t=0$) is the date and time given by parameter cut_st.	実数。 A real number.	0.0
residual_tmax	グリッドサーチにおいて残差の計算に用いる時間窓の末尾時刻$t_{max}$(s)。なおパラメータcut_stで与えた日時を時刻$t=0$とする。 The end of a time window, $t_{max}$ (s), used for the computation of residuals in a grid search. The time origin ($t=0$) is the date and time given by parameter cut_st.	パラメータresidual_tminの値よりも大きな実数。 A real number greater than the value of parameter residual_tmin.	パラメータcut_enの値に対応する時刻。 Time corresponding to the value of parameter cut_en.

(7)出力に関するパラメータ (Parameters for output)
最後に、計算結果の出力を制御するパラメータを下表にまとめる。
Finally, parameters that control outputs are shown in the table below.

多くの量を出力することで最適解だけでなくその信頼性評価に関わる様々な情報を得ることができる。しかし経験上、計算自体よりも出力に時間がかかる。したがって、特にグリッドサーチを行う場合には

出力する量を最小限(残差値のみ)としてグリッドサーチを行い、最適なソース位置や発震機構パラメータを決定する
得られた最適なソース位置と発震機構パラメータを用いて再度逆解析を行い、詳細情報を出力する

という2段階のアプローチを推奨する。
By outputting various quantities, users obtain various information not only to have the optimal solution but to evaluate its reliability. However, my experiences indicate that outputting take more time than computation itself. Therefore, a two-step approach as below is recommended, especially if you need a grid search:

perform a grid search to determine the optimal source location and focal mechanism parameters, outputting the minimum information (only the residual values), and then
repeat the inversion using the optimal source location and focal mechanism parameters, outputting more detailed information.

パラメータ名 Parameter name	意味 Meaning	可能なパラメータ値 Allowed parameter values	デフォルト値 Default value
outputdir	計算結果の出力先のディレクトリパス。 The directory path for outputting the results.	ディレクトリパスを表す文字列。 A string that represents a directory path.	inversion_result
output_residual_value	観測波形と合成波形の残差の値を出力するか否かの選択。 A choice of whether to output the values of residuals between observed and synthetic waveforms.	yes 出力する。 Output. no 出力しない。 Do not output.	yes
output_solution	震源時間関数と合成波形を出力するか否かの選択。 A choice of whether to output the source time functions and synthetic waveforms.	yes 出力する。 Output. no 出力しない。 Do not output.	yes
output_green	逆解析に用いた実用グリーン関数の時系列データを出力するか否かの選択。 A choice of whether to output the time series data of practical Green’s functions used for inversion.	yes 出力する。 Output. no 出力しない。 Do not output.	yes
output_residual	それぞれの周波数における (\ref{eq.inverse_problem})式の左辺と右辺の残差を出力するか否かの選択。 A choice of whether to output the residual between the left and right hand sides of Eq. (\ref{eq.inverse_problem}) for each frequency.	yes 出力する。 Output. no 出力しない。 Do not output.	no
output_residual_trace	観測波形と合成波形の残差の時系列データを出力するか否かの選択。 A choice of whether to output time series data between observed and synthetic waveforms.	yes 出力する。 Output. no 出力しない。 Do not output.	no
output_contribution	合成波形に対する各要素ソースからの寄与を出力するか否かの選択。 A choice of whether to output the contribution of each elementary source to synthetic waveforms.	yes 出力する。 Output. no 出力しない。 Do not output.	no
output_trans_tilt	並進運動と傾斜変動のそれぞれの合成波形を出力するか否かの選択。 A choice of whether to output each of the the synthetic translational and tilt waveforms.	yes 出力する。 Output. no 出力しない。 Do not output.	no
output_spectrum	逆解析の過程に登場する各種のフーリエスペクトルを出力するか否かの選択。 A choice of whether to output various Fourier spectra that are used in the intermediate process of inversion.	yes 出力する。 Output. no 出力しない。 Do not output.	no
output_matrix	逆解析の過程に登場する各種の行列を出力するか否かの選択。 A choice of whether to output various matrices that are used in the intermediate process of inversion.	yes 出力する。 Output. no 出力しない。 Do not output.	no
output_singular	特異値を出力するか否かの選択。 A choice of whether to output the singular values.	yes 出力する。 Output. no 出力しない。 Do not output.	no
output_Nnonzero_singular	ノンゼロ特異値の個数を出力するか否かの選択。 A choice of whether to output the number of non-zero singular values.	yes 出力する。 Output. no 出力しない。 Do not output.	yes
verbose	画面に表示する計算の進行状況の種類。 A choice of information for the progress of computation to be displayed.	0 進行状況を表示しない。 Do not display the progress. 1 発震機構パラメータのグリッドサーチの進行状況を表示する。 Display the progress of a grid search for focal mechanism parameters. 2 上記に加え、ソース位置のグリッドサーチの進行状況を表示する。 In addition to the information above, display the progress of a grid search for the source location. 3 上記に加え、逆解析の進行状況を表示する。なお、この表示を行うと処理時間が有意に増加する。 In addition to the information above, display the progress in each inversion. This option increases the processing time at unignorable level.	2

◆動作(Behaviour)

パラメータdatadirで指定したディレクトリ内の波形データとパラメータgreendirで指定したディレクトリ内の実用グリーン関数を用いて最適な震源時間関数$s_m(t)$、ソース位置、発震機構パラメータを求め、結果をパラメータoutputdirで指定したディレクトリ内に出力する。
Estimate the optimal source time functions $s_m(t)$, source location, and focal mechanism parameters using waveform data in the directory specified by parameter datadir and practical Green’s functions in the directory specified by parameter greendir. Output the results into the directory specified by parameter outputdir.

◆出力されるファイル(Output files)

「output_」から始まるパラメータの値に応じて以下のファイルが出力される。ファイル名のリンクをクリックすると詳細が表示される。
The outputs of the program are the files listed below. For detail, click the links in the file names.

ファイルが多数あって分かりにくいので主に使用するものを赤色のセルで示す。発震機構パラメータやソース位置をグリッドサーチしたときの残差の分布は residual_value.datに記録される。推定した震源時間関数はmodel/∗.seq1である。観測波形と合成波形の比較図のプロットには data_obs/∗.seq1, data_syn/∗.seq1を使用する。
Red cells indicate files that are most frequently used; residual_value.dat shows the distribution of residuals on parameter spaces of focal mechanism parameters and the assumed source location, model/∗.seq1 does the estimated source time functions, and data_obs/∗.seq1 and data_syn/∗.seq1 are used to plot figures for comparison of observed and synthetic waveforms.

●出力ディレクトリの下に直接出力されるデータや解析結果 (Data and analysis results that are written directly beneath the output directory)

下表において出力ファイル名はパラメータoutputdirで指定したディレクトリからの相対パスである。
The file names are shown as relative paths from the directory specified by parameter outputdir.

出力ファイル名 The output file name	出力されるデータ The data in the output file	出力される条件 Conditions to output
data_obs/∗.seq1	使用した観測波形$u_n^{obs}(t)$の時系列データ。 The time series data of observed waveforms $u_n^{obs}(t)$ used.	常に出力される。 Always created.
data_obs_spectrum/∗.imseq2	使用した観測波形のフーリエスペクトル$\tilde{U}_n^{obs}(\omega)$。 The Fourier spectra $\tilde{U}_n^{obs}(\omega)$ of observed waveforms used.	パラメータoutput_spectrum=yesの場合に出力される。 Created if parameter output_spectrum=yes.
stfun.seq2	実用グリーン関数の計算に用いた震源時間関数$s^{green}(t)$の時系列データ。 The time series data of a source time function $s^{green}(t)$ used for the computation of practical Green’s functions.	常に出力される。 Always created.
stfun_spectrum.imseq2	実用グリーン関数の計算に用いた震源時間関数のフーリエスペクトル$S^{green}(\omega)$。 The Fourier spectrum $S^{green}(\omega)$ of a source time function used for the computation of practical Green’s functions.	パラメータoutput_spectrum=yesの場合に出力される。 Created if parameter output_spectrum=yes.
residual_value.dat	ローパスフィルターを掛けた観測波形と合成波形の残差$E$ (\ref{eq.residual}式)。 The residual $E$ (Eq. \ref{eq.residual}) between low-passed observed and synthetic waveforms.	パラメータoutput_residual_value=yesの場合に出力される。 Created if parameter output_residual_value=yes.

●仮定した発震機構パラメータ毎に別々のサブディレクトリに出力されるデータや解析結果 (Data and analysis results that are written into sub directories for assumed values of focal mechanism parameters)

$F_p^{(m)}$や$M_{pq}^{(m)}$を定数で与える場合、パラメータoutputdirで指定したディレクトリの下に以下のファイルが直接出力される。下表において出力ファイル名はパラメータoutputdirで指定したディレクトリからの相対パスである。
If $F_p^{(m)}$ and $M_{pq}^{(m)}$ are given as constants, the files listed below are created directly beneath the directory specified by parameter outputdir. The file names shown below are relative paths from the directory specified by parameter outputdir.
$F_p^{(m)}$や$M_{pq}^{(m)}$を発震機構パラメータを含む数式で与える場合、パラメータoutputdirで指定したディレクトリの下に仮定した発震機構パラメータの値ごとのサブディレクトリが作成される。サブディレクトリ名は発震機構パラメータの名前と値を並べたものであり、複数の発震機構パラメータがある場合はそれらをアンダーバー(_)で区切って並べる。例えばa,b,cの3つの発震機構パラメータがあり、それらの値を1.2, 3.4, 5.6と仮定した場合、サブディレクトリ名はa1.2_b3.4_c5.6となる。発震機構パラメータの値をグリッドサーチするのでこのような名前を持つサブディレクトリが多数作られることになる。下表において出力ファイル名はこのサブディレクトリからの相対パスである。
If $F_p^{(m)}$ and $M_{pq}^{(m)}$ are given as equations that consist of focal mechanism parameters, a sub directory is created for each assumed values of focal mechanism parameters beneath the directory specified by parameter outputdir. The name of the sub directory is composed of the name and the assumed value of a focal mechanism parameter; if there are multiple focal mechanism parameters, they are deployed with underbars (_) as a separater. For example, if there are three focal mechanism parameters a, b, and c, and if they are assumed to be 1.2, 3.4, and 5.6, respectively, then the sub directory name is a1.2_b3.4_c5.6. Because grid searches are performed for the focal mechanism parameters, a lot of sub directories named by this rule are created. The file names shown below are relative paths from each sub directory.

出力ファイル名 The output file name	出力されるデータ The data in the output file	出力される条件 Conditions to output
residual/∗.dat	周波数毎の残差$E(\omega)$を仮定したソース位置の関数として並べたデータ。周波数毎に別々のファイルに出力される。 Frequency-dependent residuals $E(\omega)$, expressed as a function of an assumed source location. Separate files are created for individual frequencies.	パラメータoutput_residual=yesの場合に出力される。 Created if parameter output_residual=yes.

●仮定した発震機構パラメータ、ソース候補位置毎に別々のサブディレクトリに出力されるデータや解析結果 (Data and analysis results that are written into sub directories for assumed values of focal mechanism parameters and a source location)

$F_p^{(m)}$や$M_{pq}^{(m)}$を定数で与える場合、パラメータoutputdirで指定したディレクトリの下に仮定したソース位置毎のサブディレクトリが作成される。サブディレクトリ名は$x$, $y$, $z$座標(整数)を「x値y値z値」の形式で並べたものである。例えば$x=1000$, $y=2000$, $z=-3000$であればサブディレクトリ名は「x1000y2000z-3000」となる。下表において出力ファイル名はこのサブディレクトリからの相対パスである。
If $F_p^{(m)}$ and $M_{pq}^{(m)}$ are given as constants, a directory is created for each assumed source location beneath the directory specified by parameter outputdir. The name of the sub directory is composed of the values of $x$-, $y$-, and $z$-coordinates (integers) with a “xvalueyvaluezvalue” format. For example, if $x=1000$, $y=2000$, and $z=-3000$, the name of the sub directory is “x1000y2000z-3000”. The file names shown below are relative paths from this sub directory.
$F_p^{(m)}$や$M_{pq}^{(m)}$を発震機構パラメータを含む数式で与える場合、パラメータoutputdirで指定したディレクトリの下に仮定した発震機構パラメータの値ごとのサブディレクトリが作成され、更にその下に仮定したソース位置毎のサブディレクトリが作成される。サブディレクトリの命名規則はこれまでと同じである。下表において出力ファイル名はこのサブディレクトリからの相対パスである。
If $F_p^{(m)}$ and $M_{pq}^{(m)}$ are given as equations that consist of focal mechanism parameters, a sub directory is created for each assumed values of focal mechanism parameters beneath the directory specified by parameter outputdir; within this sub directory, a sub-sub directory for each assumed source location is created. The file names shown below are relative paths from this sub-sub directory.

出力ファイル名 The output file name	出力されるデータ The data in the output file	出力される条件 Conditions to output
Lambda/∗.cdm	特異値分解で得られる行列$\myvector{\Lambda}(\omega)$。周波数毎に別々のファイルに出力される。 A matrix $\myvector{\Lambda}(\omega)$ obtained by a singular value decomposition. Separate files are created for individual frequencies.	パラメータoutput_matrix=yesかつ要素ソース数が2以上の場合に出力される。 Created if parameter output_matrix=yes and the number of elementary sources is greater than or equal to 2.
UT/∗.bdm	特異値分解で得られる行列$\myvector{U}^T(\omega)$。周波数毎に別々のファイルに出力される。 A matrix $\myvector{U}^T(\omega)$ obtained by a singular value decomposition. Separate files are created for individual frequencies.	パラメータoutput_matrix=yesかつ要素ソース数が2以上の場合に出力される。 Created if parameter output_matrix=yes and the number of elementary sources is greater than or equal to 2.
V/∗.bdm	特異値分解で得られる行列$\myvector{V}(\omega)$。周波数毎に別々のファイルに出力される。 A matrix $\myvector{V}(\omega)$ obtained by a singular value decomposition. Separate files are created for individual frequencies.	パラメータoutput_matrix=yesかつ要素ソース数が2以上の場合に出力される。 Created if parameter output_matrix=yes and the number of elementary sources is greater than or equal to 2.
R/∗.bdm	モデル解像度行列 $\myvector{R}(\omega)\equiv \myvector{V_P}(\omega)\myvector{V_P}^T(\omega)$。周波数毎に別々のファイルに出力される。 A model resolution matrix $\myvector{R}(\omega)\equiv \myvector{V_P}(\omega)\myvector{V_P}^T(\omega)$ obtained by a singular value decomposition. Separate files are created for individual frequencies.	パラメータoutput_matrix=yesかつ要素ソース数が2以上の場合に出力される。 Created if parameter output_matrix=yes and the number of elementary sources is greater than or equal to 2.
d_obs/d∗.cv	観測データベクトル$\myvector{\hat{d}^{obs}}(\omega)$。周波数毎に別々のファイルに出力される。 An observed data vector $\myvector{\hat{d}^{obs}}(\omega)$. Separate files are created for individual frequencies.	パラメータoutput_matrix=yesの場合に出力される。 Created if parameter output_matrix=yes.
G/G∗.bdm	データ核$\myvector{\hat{G}}(\omega)$。周波数毎に別々のファイルに出力される。 A data kernel $\myvector{\hat{G}}(\omega)$. Separate files are created for individual frequencies.	パラメータoutput_matrix=yesの場合に出力される。 Created if parameter output_matrix=yes.
m_est/m∗.cv	推定したモデルベクトル$\myvector{\hat{m}^{est}}(\omega)$。周波数毎に別々のファイルに出力される。 An estimated model vector $\myvector{\hat{m}^{est}}(\omega)$. Separate files are created for individual frequencies.	パラメータoutput_matrix=yesの場合に出力される。 Created if parameter output_matrix=yes.
green/∗.∗.seq1	解析に用いた実用グリーン関数$d\tilde{g}_{nm}(t)/dt$ (またはその積分、エンベロープ)。 The practical Green’ functions $d\tilde{g}_{nm}(t)/dt$ (or their integrals or envelopes) used in the analysis.	パラメータoutput_green=yesの場合に出力される。 Created if parameter output_green=yes.
green_spectrum/∗.∗.imseq2	解析に用いた実用グリーン関数$d\tilde{g}_{nm}(t)/dt$ (またはその積分、エンベロープ)のフーリエスペクトル。 The Fourier spectra of practical Green’ functions $d\tilde{g}_{nm}(t)/dt$ (or their integrals or envelopes) used in the analysis.	パラメータoutput_green=yesかつoutput_spectrum=yesの場合に出力される。 Created if parameters output_green=yes and output_spectrum=yes.
number_of_nonzero_singular_values.dat	データ核$\myvector{\hat{G}}(\omega)$のノンゼロ特異値の個数。 The number of non-zero singular values of data kernels $\myvector{\hat{G}}(\omega)$.	パラメータoutput_Nnonzero_singular=yesの場合に出力される。 Created if parameter output_Nnonzero_singular=yes.
singular_values.dat	データ核$\myvector{\hat{G}}(\omega)$の特異値のリスト。 A list of singular values of data kernels $\myvector{\hat{G}}(\omega)$.	パラメータoutput_singular=yesの場合に出力される。 Created if parameter output_singular=yes.
model/∗.seq1	推定した震源時間関数$s_m^{est}(t)$。 The estimated source time functions $s_m^{est}(t)$.	パラメータoutput_solution=yesの場合に出力される。 Created if parameter output_solution=yes.
model_spectrum/∗.imseq2	推定した震源時間関数のフーリエスペクトル$S_m^{est}(\omega)$。 The Fourier spectra of the estimated source time functions $S_m^{est}(\omega)$.	パラメータoutput_solution=yesかつoutput_spectrum=yesの場合に出力される。 Created if parameters output_solution=yes and output_spectrum=yes.
data_syn/∗.seq1	合成波形$u_n^{syn}(t)$。 Synthetic waveforms $u_n^{syn}(t)$.	パラメータoutput_solution=yesの場合に出力される。 Created if parameter output_solution=yes.
data_syn_spectrum/∗.imseq2	合成波形のフーリエスペクトル$\tilde{U}_n^{syn}(\omega)$。 The Fourier spectra of synthetic waveforms $\tilde{U}_n^{syn}(\omega)$.	パラメータoutput_solution=yesかつoutput_spectrum=yesの場合に出力される。 Created if parameters output_solution=yes and output_spectrum=yes.
data_trans/∗.seq1	観測点の位置における並進運動の合成波形。 Synthetic translational waveforms at station locations.	パラメータoutput_trans_tilt=yesの場合に出力される。 Created if parameter output_trans_tilt=yes.
data_tilt/∗.seq1	観測点の位置における傾斜変動の合成波形。 Synthetic tilt waveforms at station locations.	パラメータoutput_trans_tilt=yesの場合に出力される。 Created if parameter output_trans_tilt=yes.
contribution/∗.∗.seq1	合成波形に対する各要素ソースからの寄与。 The contributions from each elementary source to synthetic waveforms.	パラメータoutput_contribution=yesの場合に出力される。 Created if parameter output_contribution=yes.
contribution_spectrum/∗.∗.imseq2	合成波形に対する各要素ソースからの寄与のフーリエスペクトル。 The Fourier spectra of the contributions from each elementary source to synthetic waveforms.	パラメータoutput_contribution=yesかつoutput_spectrum=yes の場合に出力される。 Created if parameters output_contribution=yes and output_spectrum=yes.
residual_trace.seq1	観測波形と合成波形の残差の時系列データ。 A time series data of residuals between observed and synthetic waveforms.	パラメータoutput_residual_trace=yesの場合に出力される。 Created if parameter output_residual_trace=yes.

◆使用例(Example)

波形逆解析には地震波形データや地形データが必要になる。実際のデータはこのサイトでの公開に適さないので以下では練習用に用意した架空のデータセットを用いて逆解析の手順を説明する。ユーザは実際にこの手順でコンピュータを動かして手順を試すことができる。
Waveform inversion requires data for seismic waveforms and topography. Actual data cannot be opened at this website; therefore, a virtual dataset for practice is prepared. Below, procedures for an inverse analysis with this dataset are described. Users can try these procedures with their own computers.

練習用の架空のデータセットのダウンロードと確認 (Downloading and understanding a virtual dataset for practice)
直交座標の計算 (Calculating cartesian coordinates)
実用グリーン関数の計算条件の検討 (deciding parameters for computation of practical Green’s functions)
実用グリーン関数の計算 (computing practical Green’s functions)
逆解析(1) モーメントテンソル6成分を未知数とする解析 (inversion assuming six moment tensors as unknowns)
逆解析(2) 開口クラックを仮定した解析 (inversion assuming a tensile crack source)

◆追加の情報(Additional information)

ヘッダファイルと関数(プログラマ向け) (Header files and functions; for programmers)

◆引用文献 (References)

★ は本プログラムを用いた研究成果の発表時に必ず引用すべき論文を表す。
The star (★) indicates the references that must be cited whenever a research that used this program is published or presented.

Aki K, Richards P (2002) Quantitative seismology, 2nd edn, University Science Books, Sausalito.
Auger E, D’Auria L, Martini M, Chouet B, Dawson P (2006) Real-time monitoring and massive inversion of source parameters of very long period seismic signals: An application to Stromboli Volcano, Italy, Geophys Res Lett 33, L04301. https://doi.org/10.1029/2005GL024703
Bean C, Lokmer I, O’Brien G (2008) Influence of near-surface volcanic structure on long-period seismic signals and on moment tensor inversions: simulated examples from Mount Etna, J Geophys Res 113, B08308. https://doi.org/10.1029/2007JB005468
Chouet B, Dawson P, Arciniega-Ceballos A (2005) Source mechanism of Vulcanian degassing at Popocatépetl Volcano, Mexico, determined from waveform inversions of very long period signals, J Geophys Res 110, B07301. https://doi.org/10.1029/2004JB003524
Gardner GHF, Gardner LW, Gregory AR (1974) Formation velocity and density — the diagnostic basics for stratigraphic traps. Geophysics 39(6), 770-80. https://doi.org/10.1190/1.1440465
★ Maeda Y, Takeo M, Ohminato T (2011) A waveform inversion including tilt: method and simple tests, Geophys J Int 184(2), 907-918. https://doi.org/10.1111/j.1365-246X.2010.04892.x
Menke W (1989) Geophysical Data Analysis: Discrete Inverse Theory (Revised Edn), Academic Press, Inc.
Nakano M, Kumagai H (2005) Waveform inversion of volcano-seismic signals assuming possible source geometries, Geophys Res Lett 32, L12302. https://doi.org/10.1029/2005GL022666
Ohminato T, Chouet BA (1997) A free-surface boundary condition for including 3D topography in the finite-difference method, Bull Seism Soc Am 87, 494-515. https://doi.org/10.1785/BSSA0870020494
Ohminato T, Chouet BA, Dawson P, Kedar S (1998) Waveform inversion of very long period impulsive signals associated with magmatic injection beneath Kilauea volcano, Hawaii, J Geophys Res 103(B10), 23839-23862. https://doi.org/10.1029/98JB01122
Scherbaum F (2001) Of Poles and Zeros: Fundamentals of Digital Seismology, 2nd edn, Springer.

winvコマンド マニュアル