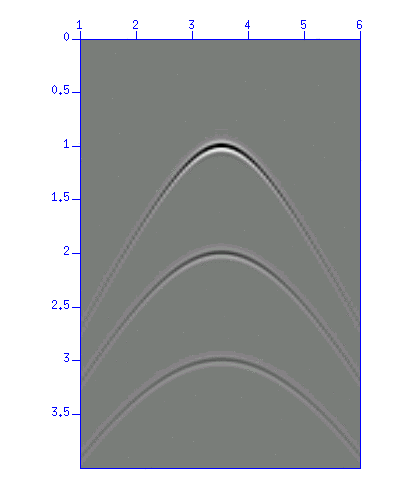
まず、demo_mig1.su のデータを表示する。
$ suximage < demo_mig1.su &

図:demo_mig1.su のイメージ表示。縦軸は時間、横軸は震源・受振点位置。
これは、深度の異なる3つの散乱点が存在する場合に得られるゼロオフセット記録である。
まず、データの中身(ヘッダの範囲)をチェックする。
$ surange < demo_mig1.su 101 traces: tracl 1 101 (1 - 101) tracr 1 101 (1 - 101) cdp 1 101 (1 - 101) % CDPの範囲は 1 - 101 cdpt 1 trid 1 sx 0 5000 (0 - 5000) gx 0 5000 (0 - 5000) counit 1 ns 201 dt 19999 % dt = 2 (ms) のはずだったが何か変。気にしなくてよい。 d2 0.050000 % CDP間隔 = 0.05 (km) = 50 (m)マイグレーションの手法はたくさんあるが、今回は f-k マイグレーションを拡張 した Stolt (1978) の方法を使う。 最大の理由は「計算時間が短くてすぐに結果が出るから」。マイグレーションは 通常時間のかかる処理である。
$ sustolt cdpmin=1 cdpmax=101 tmig=2 vmig=???? dxcdp=50 < demo_mig1.su | suximage &
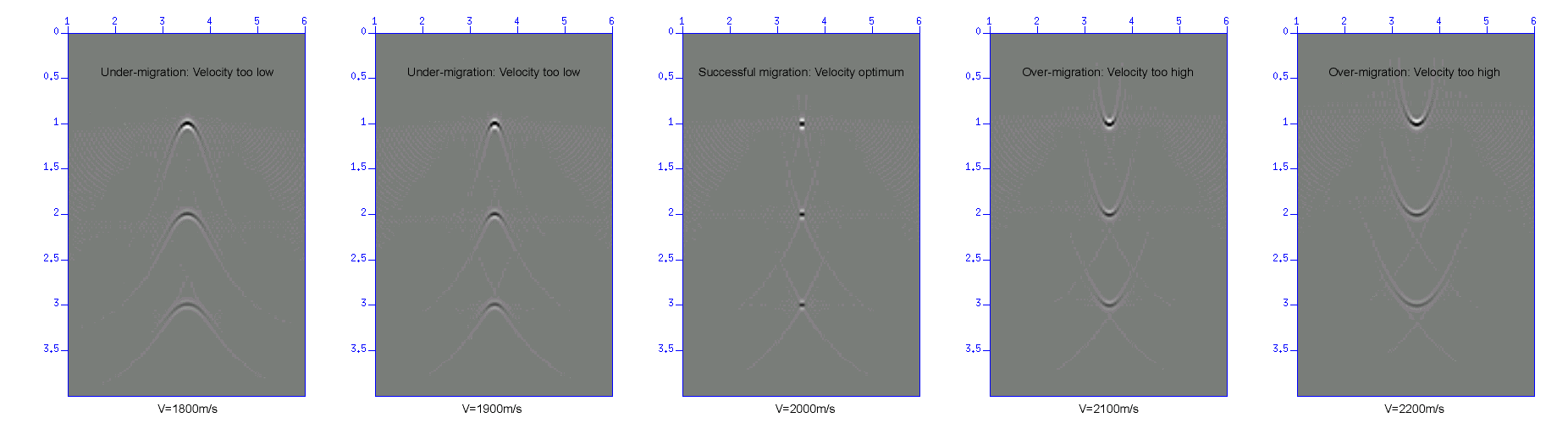
図:vmig=1800, 1900, 2000, 2100, 2200 m/sとしたマイグレーション結果。
結果を比べてみよう。
次に、demo_mig2.su も同様にマイグレーションしてみよう。ただし、速度は与えていない(ヒント:一定速度)ので、適切な速度を探すように。 手動で試行錯誤を繰り返してもよいが、課題その4で使用したシェルスクリプトを修正して使うのは非常によいアイディアである。


図:(左)demo_mig2.su のイメージ表示。(右)マイグレーション結果のイメージ表示。
マイグレーション結果のイメージから、
次に、demo_mig3.su も同様にマイグレーションしてみよう。
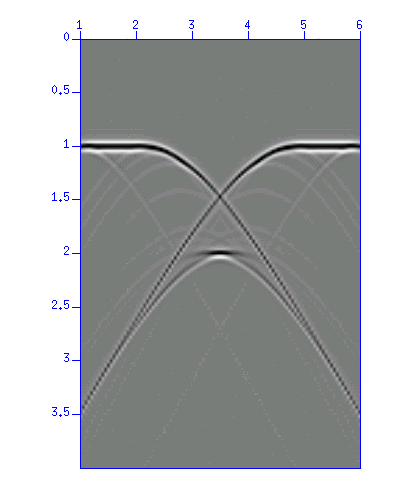
図:demo_mig3.suのイメージ表示。
これも、速度は一定であるが与えていないので、適切な速度を探すように。回折波が十分に収束する速度を選択する必要がある。 一見正解と勘違いする間違った答えを導きやすいので、十分に検討してほしい。
次に、demo_mig4.suをマイグレーションする。
demo_mig4.suを表示する。
$ suximage < demo_mig4.su &
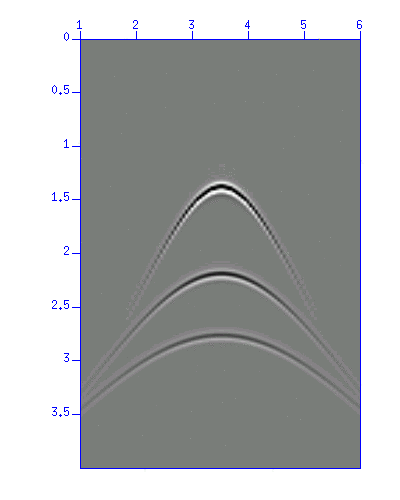
図:demo_mig4.suのイメージ表示。
demo_mig4.su の波形は demo_mig1.su と非常によく似ている。 これも深度の異なる3つの反射点が存在するモデルで得られた記録である。 これをマイグレーションしてみよう。
$ sustolt cdpmin=1 cdpmax=101 tmig=2 vmig=???? dxcdp=50 < demo_mig4.su | suximage &vmig=1400〜2500 m/s 程度を入れて結果を比較しよう。 この手の作業を行うには、課題その4で使用したシェルスクリプトを修正して使うのがよいアイディアである。
やってみるとわかるように、3つの回折波形が散乱点に収束する速度が異なる。 これは地下の速度構造が一定ではないためである。
Stolt (1978) のマイグレーションは1次元速度構造に対して拡張がなされており、深度方向の速度変化を取り扱うことができる。
$ sustolt cdpmin=1 cdpmax=101 vmig=1400,1500,1600,1700,..... tmig=1.0,1.5,2.0,2.5,..... dxcdp=50 < demo_mig4.su | suximage &

図:demo_mig4.suのマイグレーション結果。少し試すとこの程度の結果が得られるはず。