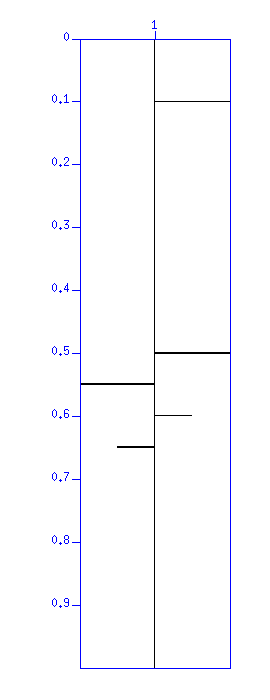
反射法では、
まず、反射係数列 demo_imp.su を表示する。
$ suxwigb < demo_imp.su &

図:反射係数列。縦軸は時間 (s)。
バイブロサイス発震で用いられるスィープ波形(時間とともに周波数が変化する波形)を作成し表示する。
$ suvibro f1=10 f2=100 tv=1 t1=0.1 t2=0.1 dt=0.001 > tmp_vib.su $ suxwigb < tmp_vib.su &
$ suacor < tmp_vib.su ntout=201 | sushw key=delrt a=-100 | suxwigb & $ suacor < tmp_vib.su ntout=201 sym=0 | suxwigb &
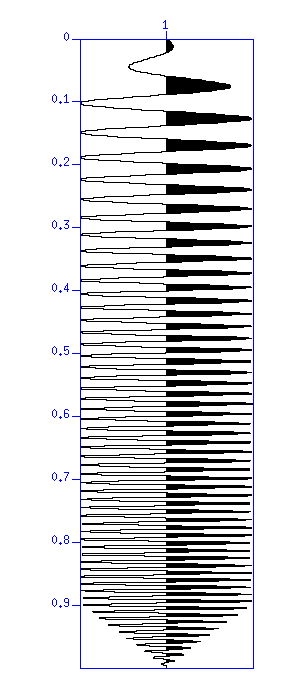
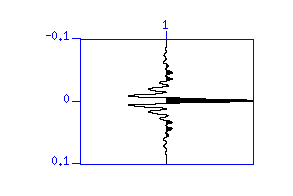
図:(左)10〜100 Hz のスィープ波形。縦軸は時間 (s)。(右)その自己相関。縦軸はラグ時間 (s)。
$ suconv sufile=tmp_vib.su < demo_imp.su > tmp_cnv.su $ suxwigb < tmp_cnv.su & $ suaddnoise sn=10 < tmp_cnv.su > tmp_cnv_noise.su $ suxwigb < tmp_cnv_noise.su &中間結果を出力する必要がなければ、コマンドをパイプで接続してもよい。
$ suconv sufile=tmp_vib.su < demo_imp.su | suaddnoise sn=10 > tmp_cnv_noise.su $ suxwigb < tmp_cnv_noise.su &
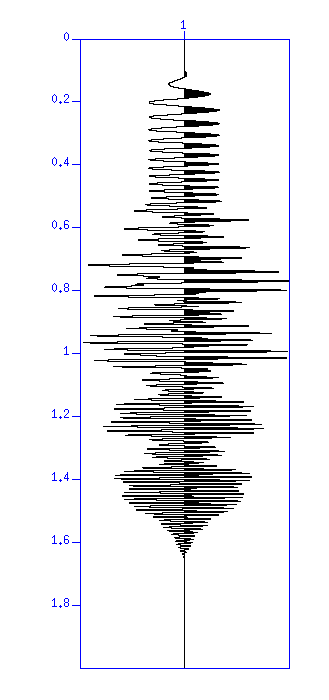
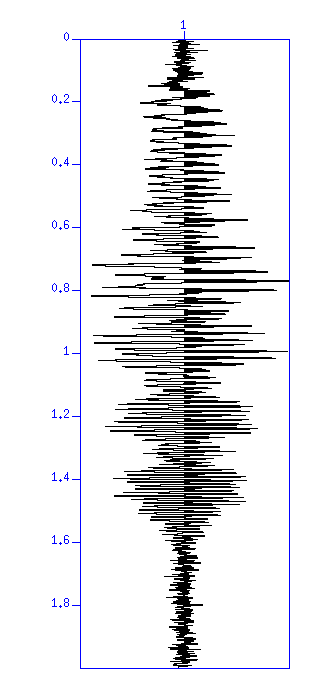
図:(左)コンボリューションした結果、ノイズなし。縦軸は時間 (s)。(右) コンボリューションした結果+ノイズ。
バイブロサイス発震の時にはこのような波形記録が観測されることになる。 そこで、この観測波形記録から反射係数列を推定することがここでの目的である。
波形記録と元のスィープ波(震源波形)の相互相関を計算する。
$ suxcor sufile=tmp_vib.su < tmp_cnv.su | suxwigb &
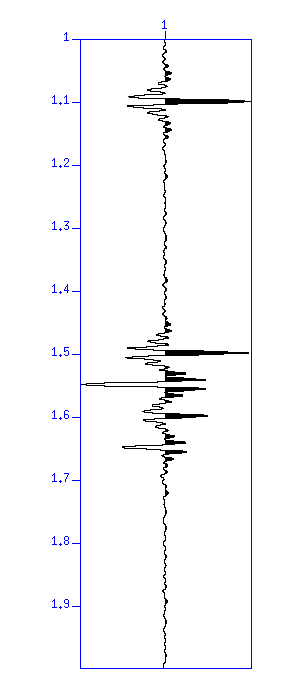

図:(左)相互相関の結果、ノイズなし。縦軸は時間 (s)。(右) 元の反射係数列。
線形の応答モデルでは、
地震波形 xcor 震源波形 =(震源波形 * 反射係数列 + ノイズ) xcor 震源波形 =(震源波形 * 反射係数列) xcor 震源波形 + ノイズ xcor 震源波形 ≒(震源波形 xcor 震源波形) * 反射係数列 = 震源波形の自己相関 (Clauder Wavelet) * 反射係数列
まず、サンプルデータ demo_dcn.su の波形と自己相関を表示する。
$ suxwigb < demo_dcn.su & $ suacor < demo_dcn.su | sushw key=delrt a=-200 | suxwigb &
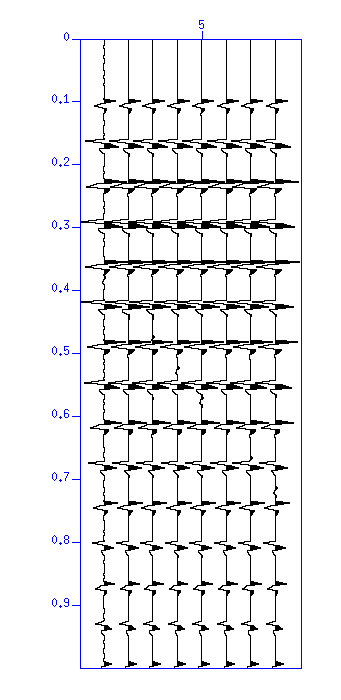
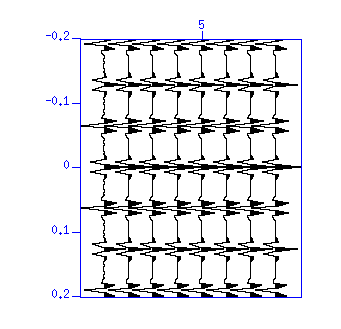
図:(左)波形。縦軸は時間 (s)。(右)自己相関。縦軸はラグ時間 (s)。
波形と自己相関を見ると、振幅の大きい繰り返し(よく見ると正負反転している) が卓越していることがわかる。これは下図に示すような、 浅海の記録でよく見られる水中を多重反射した波(水中残響という)を含む記録の例である (多重反射をするたびに走時が 2t だけ遅れ、海面で反射するたびに正負が反転する)。
微弱な反射波はこれらに隠されてしまうので、水中残響を取り除くことが必要である。
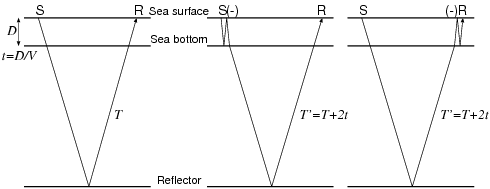
図:水中残響の模式図。
まず、波形をパルス(スパイク)に変換するデコンボリューションフィルタを適用する。結果と自己相関を表示する。
$ supef < demo_dcn.su maxlag=???? > tmp_decon.su $ suxwigb < tmp_decon.su & $ suacor < tmp_decon.su | sushw key=delrt a=-200 | suxwigb &
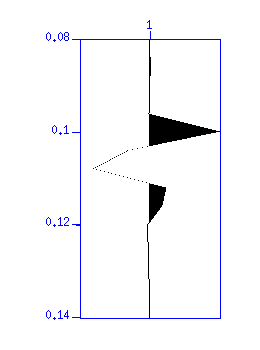
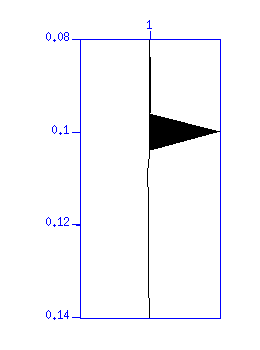
図:(左)元の波形(拡大)(右)デコンボリューションの結果(拡大)。
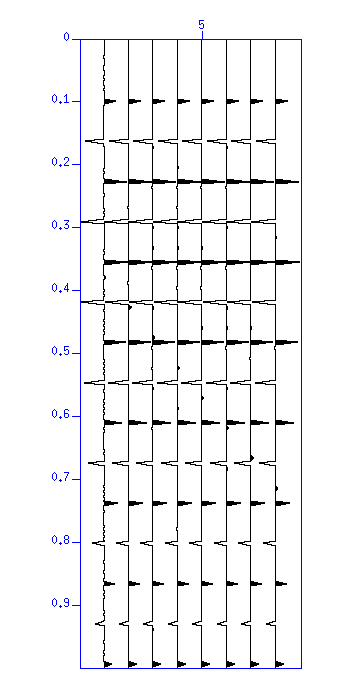
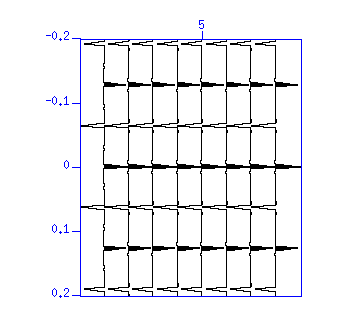
図:(左)デコンボリューションの結果の波形。縦軸は時間 (s)。(右)その自 己相関。縦軸はラグ時間 (s)。波形がパルス(スパイク)状に変換されたことは 自己相関を見てもわかる。
次に、繰り返しを除去する予測誤差フィルタを適用する。
$ supef minlag=???? maxlag=???? < tmp_decon.su | suxwigb & $ supef minlag=???? maxlag=???? < tmp_decon.su | suacor | sushw key=delrt a=-200 | suxwigb &繰り返しの時間間隔に関するフィルタのパラメータ minlag, maxlag は、フィールドデータでは経験的に下図のように自己相関の形状から推定することが一般的である。しかし、必ずうまくいくとは限らないので、ある程度の試行錯誤が必要である。

minlag, maxlagには
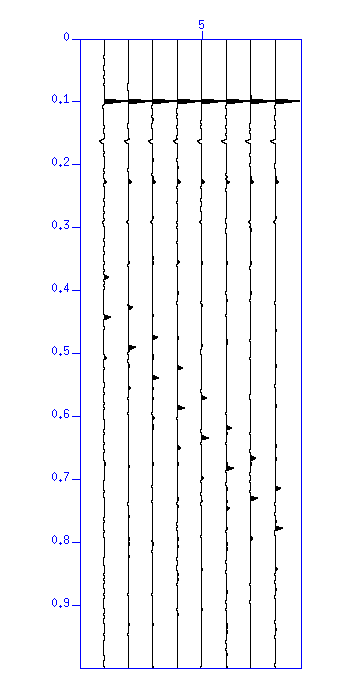
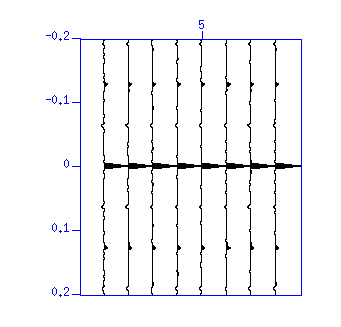
図:(左)デコンボリューションの結果の波形。縦軸は時間 (s)。(右)その自 己相関。縦軸はラグ時間 (s)。波形の繰り返しが除去されたことは自己相関がパルス状になっていることを見てもわかる。
実際のデータ処理では、デコンボリューションを適用した後にバンドパスフィルタを適用する。 その主な理由は、(ホワイトニング)デコンボリューションによって白色化(広帯域化)したスペクトルを元の周波数帯域に戻すためである。