
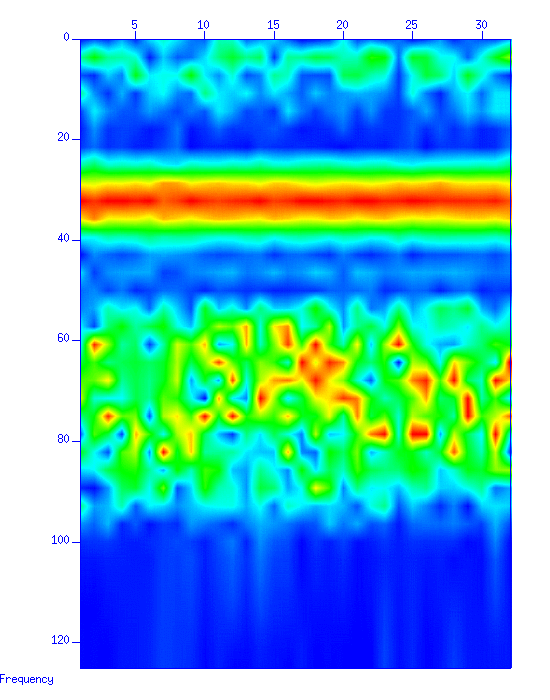
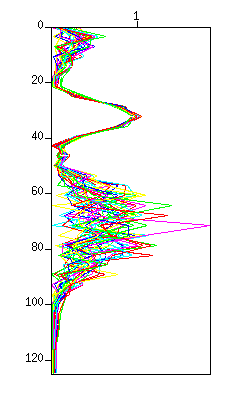
まず、波形を表示する。
$ suxwigb < demo_bpf.su perc=98 &スペクトルを計算して表示する。
$ suspecfx < demo_bpf.su | suximage perc=98 & $ suspecfx < demo_bpf.su | suxgraph & $ suspecfx < demo_bpf.su | suop op=db | suxgraph &



図:(左)波形。縦軸は時間 (s)、横軸はトレース、(中)スペクトル(カラーイメージ表示)。縦軸は周波数 (Hz)、横軸はトレース、(右)スペクトル(グラフ表示)、横軸はリニア表示。
フィルタをかけて表示してみよう。
スペクトルから、データには大きく分けて 0〜20 Hz, 20〜40 Hz, 50〜100 Hz の3つの 周波数帯域のデータが混在していることがわかる。そこで下図のようなフィルタ を適用する。
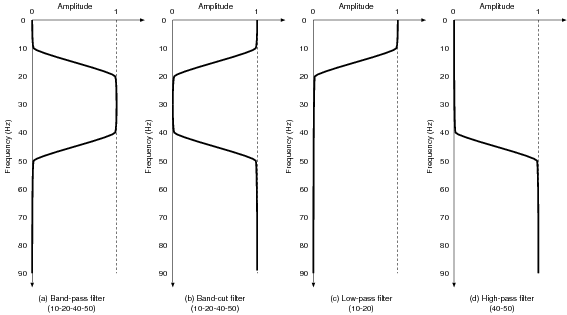
まず、(a)のバンドパスフィルタを適用し、20〜40 Hzの信号を取り出す。
$ sufilter f=10,20,40,50 amps=0,1,1,0 < demo_bpf.su | suxwigb & $ sufilter f=10,20,40,50 amps=0,1,1,0 < demo_bpf.su | suspecfx | suxgraph &

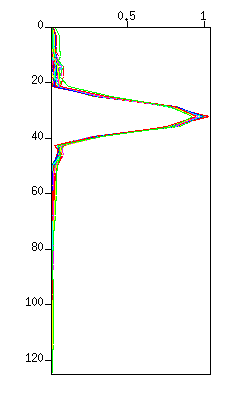
図:(左)波形。縦軸は時間 (s)、横軸はトレース、(右)スペクトル(グラフ表示)、横軸はリニア表示。
20〜40 Hz の信号のみが残っていることを確認しよう。
(b)は(a)のバンドパスフィルタの帯域を削除するフィルタ。'amps= 'の指定方法が逆になっていることに注意しよう。
$ sufilter f=10,20,40,50 amps=1,0,0,1 < demo_bpf.su | suxwigb & $ sufilter f=10,20,40,50 amps=1,0,0,1 < demo_bpf.su | suspecfx | suxgraph &

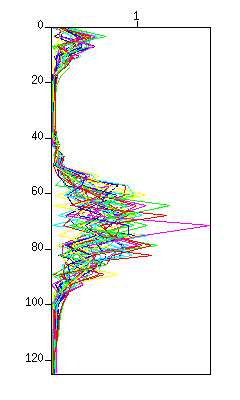
図:(左)波形。縦軸は時間 (s)、横軸はトレース、(右)スペクトル(グラフ表示)、横軸はリニア表示。
先ほどとは逆に、20〜40 Hzの信号が除去されていることを確認しよう。
(c), (d)はそれぞれローパスフィルタ、ハイパスフィルタ。
$ sufilter f=10,20 amps=1,0 < demo_bpf.su | suxwigb & $ sufilter f=10,20 amps=1,0 < demo_bpf.su | suspecfx | suxgraph & $ sufilter f=40,50 amps=0,1 < demo_bpf.su | suxwigb & $ sufilter f=40,50 amps=0,1 < demo_bpf.su | suspecfx | suxgraph &

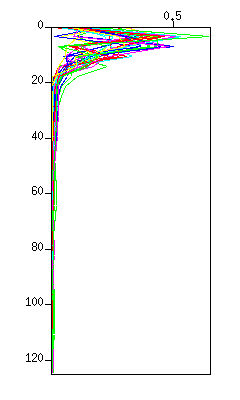
図:(左)波形。縦軸は時間 (s)、横軸はトレース、(右)スペクトル(グラフ表示)、横軸はリニア表示。

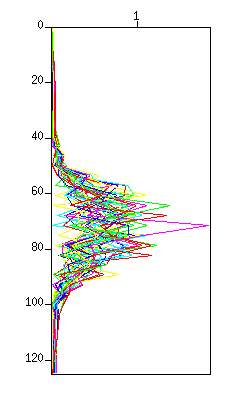
図:(左)波形。縦軸は時間 (s)、横軸はトレース、(右)スペクトル(グラフ表示)、横軸はリニア表示。
(c)では20 Hz以下の低周波数信号が、(d)では40Hz以上の高周波数信号が取り出されていることを確認する。
まず、波形を表示する。
$ suxwigb < demo_fkf.su &見かけ速度の異なる3種類の波が同時に観測されている。それぞれの波がある点で重なっていることに注意する。
2重フーリエ変換して時間-距離(t-x)のデータを周波数-波数に変換した f-k スペクトルを計算して表示する。
$ suspecfk < demo_fkf.su | suximage &
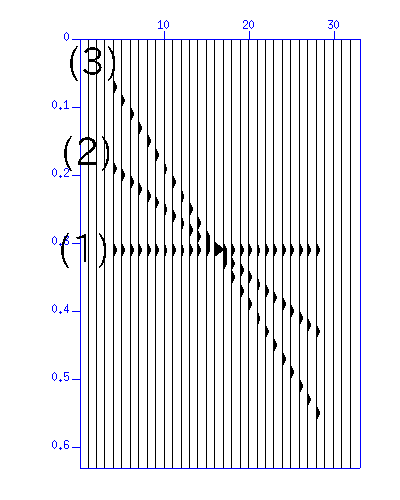
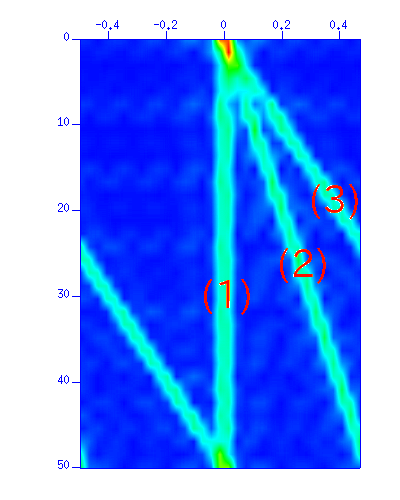
図:(左)波形。縦軸は時間 (s)、横軸は距離 (m)、(右)f-kスペクトルのカラー表示。縦軸は周波数 (Hz)、横軸は波数 (1/m)
t-x平面の(1),(2),(3)の波はf-k平面上ではそれぞれ対応する位置に表示される。 (3)の波は空間エリアシングしている(波数領域でスペクトルの回り込みがある:右端の部分が左端に続く)ことがわかる。
速度フィルタをかけてみる。 t-x平面で (1), (2), (3) の波の傾き(dt/dx)はそれぞれ 0.00, 0.01, 0.02 であることが見て取れる。
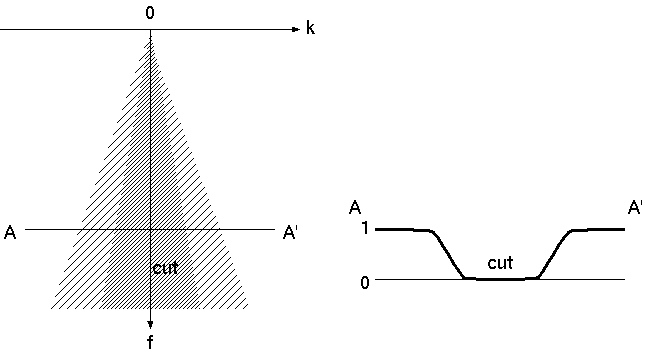
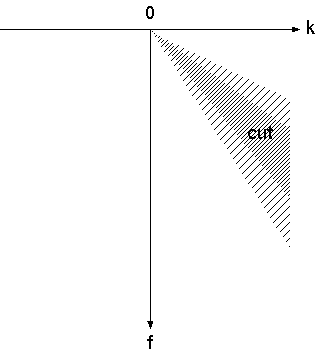
まず(1)の波を消去する。t-x平面で傾き(dt/dx)が 0 (すなわち見かけ速度が∞)なので、傾きが 0 付近 (-0.005~0.005) の波を除去するフィルタを適用する。 f-k平面では下図のようなフィルタに相当する(斜線の濃い部分をカットする)。
$ sudipfilt slopes=-0.01,-0.005,0.005,0.01 amps=1,0,0,1 < demo_fkf.su | suxwigb & $ sudipfilt slopes=-0.01,-0.005,0.005,0.01 amps=1,0,0,1 < demo_fkf.su | suspecfk | suximage &
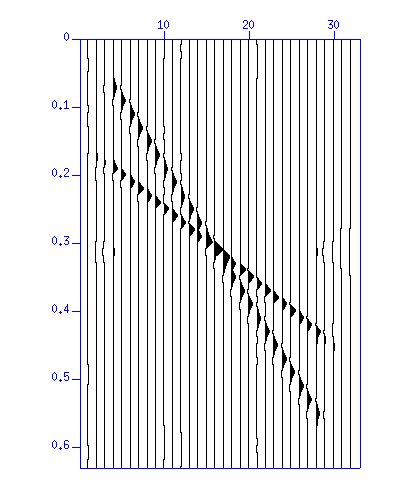
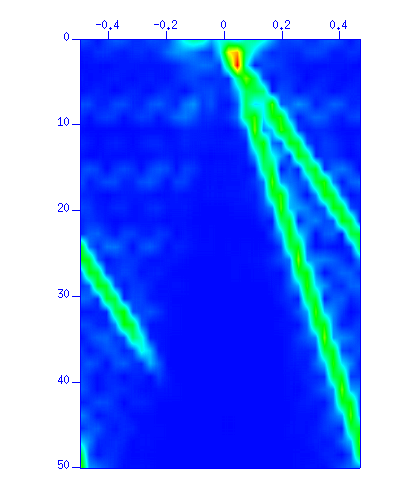
図:(左)波形。縦軸は時間 (s)、横軸は距離 (m)、(右)f-kスペクトルのカラー表示。縦軸は周波数 (Hz)、横軸は波数 (1/m)
次に(3)の波を消去してみよう。t-x 平面で(3)の波は傾き(dt/dx)が 0.02 なので、傾きが 0.02 付近 (0.0175~0.0225) の波を除去するフィルタを適用する。 f-k平面では下図のようなフィルタに相当する。
$ sudipfilt slopes=0.015,0.0175,0.0225,0.025 amps=1,0,0,1 < demo_fkf.su | suxwigb & $ sudipfilt slopes=0.015,0.0175,0.0225,0.025 amps=1,0,0,1 < demo_fkf.su | suspecfk | suximage &
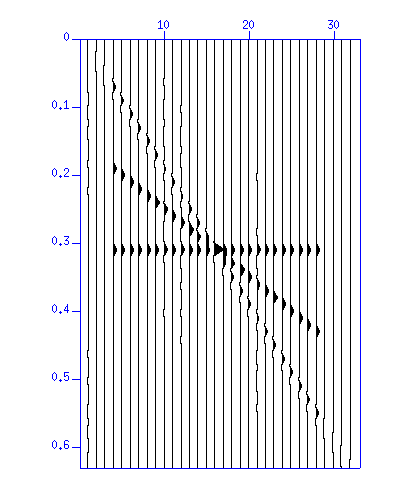
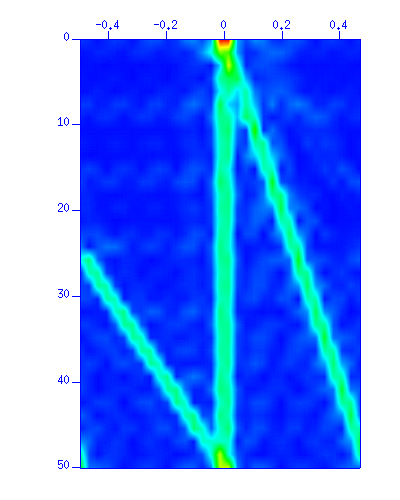
図:(左)波形。縦軸は時間 (s)、横軸は距離 (m)、(右)f-kスペクトルのカラー表示。縦軸は周波数 (Hz)、横軸は波数 (1/m)
t-x 平面上の波形を見ると、消去したはずの(3)の波が少し残っていることがわかる。この理由は f-k 平面を見ると明らかで、 今回適用したフィルタではエリアシングした部分(左側に回り込んでいる部分)を削除していないので、これが残っているためである。 (これを削除するには、さらに傾きが負の部分を削除するフィルタを適用する等の必要がある)。 このように、空間エリアシングが生じるとデータ処理上問題が生じるので、観測点間隔や観測点数に配慮が必要である。
sudipfilt slopes=(切り取る傾きを図から読み取る) amps=(フィルタの形状を指定する) < demo_fkf2.su | .............波形表示の縦軸から時間、横軸から距離を読んで傾き(dt/dx)を求め、'slopes= 'に与えるパラメータを指定しなさい。
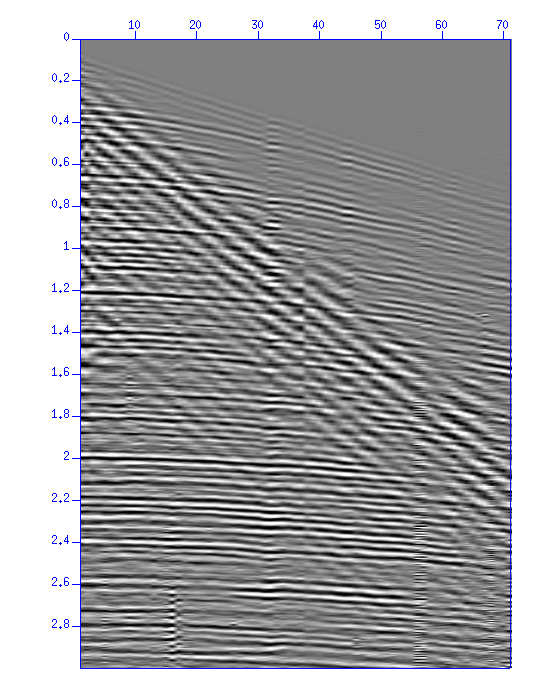
図:(左)サンプルデータ demo_fkf2.su の表示。縦軸は時間 (s)、横軸は距離 (m)、(右)
ちなみに、逆に表面波だけを残すと下図のようになる。
